New Paper on Sars-CoV-2

Phase transitions may explain why SARS-CoV-2 spreads so fast and why new variants are spreading faster

J.C.Phillips, Marcelo A.Moret, Gilney F.Zebende, Carson C.Chow

Abstract

The novel coronavirus SARS CoV-2 responsible for the COVID-19 pandemic and SARS CoV-1 responsible for the SARS epidemic of 2002-2003 share an ancestor yet evolved to have much different transmissibility and global impact ¹. A previously developed thermodynamic model of protein conformations hypothesized that SARS CoV-2 is very close to a new thermodynamic critical point, which makes it highly infectious but also easily displaced by a spike-based vaccine because there is a tradeoff between transmissibility and robustness ². The model identified a small cluster of four key mutations of SARS CoV-2 that predicts much stronger viral attachment and viral spreading compared to SARS CoV-1. Here we apply the model to the SARS-CoV-2 variants Alpha (B.1.1.7), Beta (B.1.351), Gamma (P.1) and Delta (B.1.617.2)³ and predict, using no free parameters, how the new mutations will not diminish the effectiveness of current spike based vaccines and may even further enhance infectiousness by augmenting the binding ability of the virus.

https://www.sciencedirect.com/science/article/pii/S0378437122002576?dgcid=author

This paper is based on the ideas of physicist Jim Phillips, (formerly of Bell Labs, a National Academy member, and a developer of the theory behind Gorilla Glass used in iPhones). It was only due to Jim’s dogged persistence and zeal that I’m even on this paper although the persistence and zeal that ensnared me is the very thing that alienates most everyone else he tries to recruit to his cause.

Jim’s goal is to understand and characterize how a protein will fold and behave dynamically by utilizing an amino acid hydrophobicity (hydropathy) scale developed by Moret and Zebende. People have been developing hydropathy scores for many decades as a way to understand proteins with the idea that hydrophobic amino acids (residues) will tend to be on the inside of proteins while hydrophillic residues will be on the outside where the water is. There are several existing scores but Moret and Zebende, who are physicists and not chemists, took a different tack and found how the solvent-accessible surface area (ASA) scales with the size of a protein fragment with a specific residue in the center. The idea being that the smaller the ASA the more hydrophobic the residue. As protein fragments get larger they will tend to fold back on themselves and thus reduce the ASA. They looked at several thousand protein fragments and computed the average ASA with a given amino acid in the center. When they plotted the ASA vs length of fragment they found a power law and each amino acid had its own exponent. The more negative the exponent the smaller the ASA and thus the more hydrophobic the residue. The (negative) exponent could then be used as a hydropathy score. It differs from other scores in that it is not calculated in isolation based on chemical properties but accounts for the background of the amino acid.

M and Z’s score blew Jim’s mind because power laws are indicative of critical phenomena and phase transitions. Jim computed the coarse-grained hydropathy score (over a window of 35 residues) at each residue of a protein for a number of protein families. When COVID came along he naturally applied it to coronaviruses. He found that the coarse-grained hydropathy score profile of the spike protein of SARS-CoV-1 and SARS-CoV-2 had several deep hydrophobic wells. The well depths were nearly equal with SARS-CoV-2 being more equal than SARS-CoV-1. He then hypothesized that there was a selection advantage for well-depth symmetry and evolutionary pressure had pushed the SARS-CoV-2 spike to be near optimal. He argues that the symmetry allows the protein to coordinate activity better much like the way oscillators synchronize easier if their frequencies are more uniform. He predicted that given this optimality the spike was fragile and thus spike vaccines would be highly effective and that spike mutations could not change the spike much without diminishing function.

My contribution was to write some Julia code to automate this computation and apply it to some SARS-CoV-2 variants. I also scanned window sizes and found that the well depths are most equal close to Jim’s original value of 35. Below is Figure 3 from the paper.

Figure 3.  Hydropathy score Ψ(R,W) for CoV-1, CoV-2, Alpha, and Delta, at the optimal W. The six local hydropathic minima (hydrophilic maxima) are much more symmetric in CoV-2 and variants compared to CoV-1. Minimum 1 is located within the RBD (residues 331-524), which also contains other local minima and maxima.

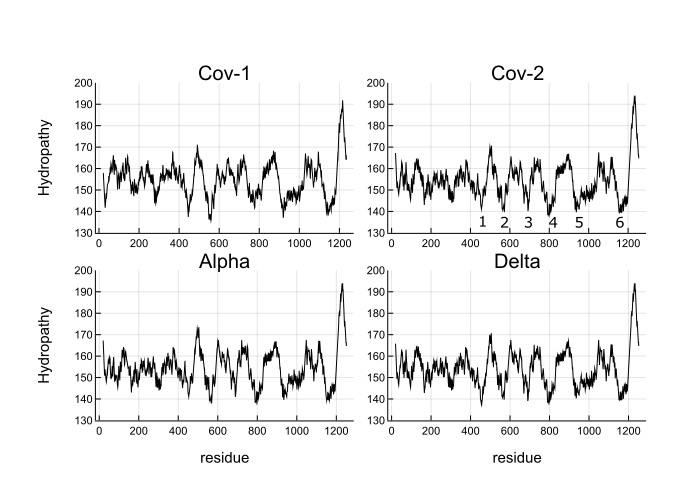
What you see is the coarse-grained hydropathy score of the spike protein which is a little under 1300 residues long. Between residue 400 and 1200 there are 6 hydropathic wells. The well depths are more similar for SARS-CoV-2 and variants than SARS-CoV-1. Omicron does not look much different from the wild type, which makes me think that Omicron’s increased infectiousness is probably due to mutations that affect viral growth and transmission rather than spike binding to ACE2 receptors.

Jim is encouraging (strong arming) me into pushing this further, which I probably will given that there are still so many unanswered questions as to how and why it works, if at all. If anyone is interested in this, please let me know.

Talk at Howard

Here are the slides for my talk at the “Howard University Math-Bio Virtual Workshop on Mitigation of Future Pandemics”  last Saturday. One surprising thing (to me) the model predicted, shown on slide 40, is that the median fraction of those previously infected or vaccinated (or both) was 40% or higher during the omicron wave. I was pleased and relieved to then find that recent CDC serology results validate this prediction.

howardDownload

Reorganizing risk in the age of disaster

I’ve been thinking a lot about what we should do for the next (and current) disaster. The first thing to say is that I am absolutely positively sure that I could not have done any better than what had been done for Covid-19. I probably would have done things differently but I doubt it would have led to a better (and probably a worse) outcome. I still think in aggregate, we are doing about as well as we could have. The one thing I do think we need to do is to figure out a way to partition risk. The biggest problem of the current pandemic is that people do not realize or care that their own risky behavior puts other people at risk. I do not care if a person wants to jump off of a cliff in a bat suit because they are mostly taking the risk upon themselves (although they do take up a bed in an ER ward if they get injured). However, not wearing a mask or getting vaccinated puts other people, including strangers, at risk. If you knowingly attend a wedding with a respiratory illness then you have the potential to infect tens if not hundreds of people and killing a fraction of them.

I do think people should be allowed to take risks as long as there are limited consequences to others. Thus, in a pandemic I think we should figure out a way for people to not get vaccinated or wear masks without affecting others. Currently, the main bottleneck is the health care system. If we allow people to wantonly get infected then there is a risk that they overwhelm hospitals. This affects all people who may need healthcare. Now is not a good time to try to repair your roof because if you fall you may not be able to get a bed in an ER ward. Thus, we really do need to think about stratifying health care according to risk acceptance. People who choose to lead risky lives should get to the back of the line when it comes to treatment. These policies should be made clear. Those who refuse to be vaccinated should just sign a form that they could be delayed in receiving health care. If you want to attend a large gathering then you should sign the same waiver.

I think that people should be allowed to opt out of the Nanny State but they need to absorb the consequences. I personally like to live in a highly regulated state but I think people should have a choice to opt out. They can live in a flood zone if they wish but they should not be bailed out after the flood. If banks want to participate in risky activities then fine but we should not bail them out. We should have let every bank fail after the 2008 crisis. We could have just let them all go under and saved homeowners instead (who should have been made better aware of the risks they were taking). Bailing out banks was a choice not a necessity.

The dynamics of breakthrough infections

In light of the new omicron variant and breakthrough infections in people who have been vaccinated or previously infected, I was asked to discuss what a model would predict. The simplest model that includes reinfection is an SIRS model, where R, which stands for recovered, can become susceptible again. The equations have the form

I have ignored death due to infection for now. So like the standard SIR model, susceptible, S, have a chance of being infected, I, if they contact I. I then recovers to R but then has a chance to become S again. Starting from an initial condition of S = N and I very small, then S will decrease as I grows.

The first thing to note that the number of people N is conserved in this model (as it should be). You can see this by noting that the sum of the right hand sides of all the equations is zero. Thus and thus the integral is a constant and given that we started with N people then there will remain N people. This will change if we include births and deaths. Given this conservation law, then the dynamics have three possibilities. The first is that it goes to a fixed point meaning that in the long run the numbers of S, I and R will stabilize to some fixed number and remain there forever. The second is that it oscillates so S, I, and R will go up and down. The final one is that the orbit is chaotic meaning that S, I and R will change unpredictably. For these equations, the answer is the first option. Everything will settle to a fixed point.

To show this, you first must find an equilibrium or fixed point. You do this by setting all the derivatives to zero and solving the remaining equations. I have always found the fixed point to be the most miraculous state of any dynamical system. In a churning sea where variables move in all directions, there is one place that is perfectly still. The fixed point equations satisfy

There is a trivial fixed point given by S = N and I = R = 0. This is the case of no infection. However, if is large enough then this fixed point is unstable and any amount of I will grow. Assuming I is not zero, we can find another fixed point. Divide I out of the second equation and get

Solving the third equation gives us

which we can substitute into the first equation to get back the second equation. So to find I, we need to use the conservation condition S + I + R = N which after substituting for S and R gives

which we then back substitute to get

The fact that and must be positive implies is necessary.

The next question is whether this fixed point is stable. Just because a fixed point exists doesn’t mean it is stable. The classic example is a pencil balancing on its tip. Any small perturbation will knock it over. There are many mathematical definitions of stability but they essentially boil down to – does the system return to the equilibrium if you move away from it. The most straightforward way to assess stability is to linearize the system around the fixed point and then see if the linearized system grows or decays (or stays still). We linearize because linear systems are the only types of dynamical systems that can always be solved systematically. Generalizable methods to solve nonlinear systems do not exist. That is why people such as myself can devote a career to studying them. Each system is its own thing. There are standard methods you can try to use but there is no recipe that will always work.

To linearize around a fixed point we first transform to a coordinate system around that fixed point by defining , , , to get

So now s = h = r = 0 is the fixed point. I used lower case h because lower case i is usually . The only nonlinear term is , which we ignore when we linearize. Also by the definition of the fixed point the system then simplifies to

which we can write as a matrix equation

, where and . The trace of the matrix is so the sum of the eigenvalues is negative but the determinant is zero (since the rows sum to zero), and thus the product of the eigenvalues is zero. With a little calculation you can show that this system has two eigenvalues with negative real part and one zero eigenvalue. Thus, the fixed point is not linearly stable but could still be nonlinearly stable, which it probably is since the nonlinear terms are attracting.

That was a lot of tedious math to say that with reinfection, the simplest dynamics will lead to a stable equilibrium where a fixed fraction of the population is infected. The fraction increases with increasing or and decreases with . Thus, as long as the reinfection rate is much smaller than the initial infection rate (which it seems to be), we are headed for a situation where Covid-19 is endemic and will just keep circulating around forever. It may have a seasonal variation like the flu, which is still not well understood and is beyond the simple SIRS equation. If we include death in the equations then there is no longer a nonzero fixed point and the dynamics will just leak slowly towards everyone dying. However, if the death rate is slow enough this will be balanced by births and deaths due to other causes.

My immune system

One outcome of the pandemic is that I have not had any illness (knock on wood), nary a cold nor sniffle, in a year and a half. On the other hand, my skin has fallen apart. I am constantly inflamed and itchy. I have no proof that the two are connected but my working hypothesis is that my immune system is hypersensitive right now because it has had little to do since the spring of 2020. It now overreacts to every mold spore, pollen grain, and speck of dust it runs into. The immune system is extremely complex, perhaps as complex as the brain. Its job is extremely difficult. It needs to recognize threats and eliminate them while not attacking itself. The brain and the immune system are intricately linked. How many people have gotten ill immediately after a final exam or deadline? The immune system was informed by the brain to delay action until the task was completed. The brain probably takes cues form the immune system too. One hypothesis for why asthma and allergies have been on the rise recently is that modern living has eliminated much contact with parasites and infectious agents, making the immune system hypersensitive. I for one, always welcome vaccinations because it gives my immune system something to do. In fact, I think it would be a good idea to get inoculations of all types regularly. I would take a vaccine for tape worm in a heartbeat. We are now slowly exiting from a global experiment in depriving the immune system of stimulation. We have no idea what the consequences will be. That is not to say that quarantine and isolation was not a good idea. Being itchy is clearly better than being infected by a novel virus (or being dead). There can be long term effects of infection too. Long covid is likely to be due to a miscalibrated immune system induced by the infection. Unfortunately, we shall likely never disentangle all the effects of COVID-19. We will not ever truly know what the long term consequences of infection, isolation, and vaccination will be. Most people will come out of this fine but a small fraction will not and we will not know why.

RNA

I read an article recently about an anti-vaccination advocate exclaiming at a press conference with the governor of Florida that vaccines against SARS-CoV-2 “change your RNA!” This made me think that most people probably do not know much about RNA and that a little knowledge is a dangerous thing. Now ironically, contrary to what the newspapers say, this statement is kind of true although in a trivial way. The Moderna and Pfizer vaccines insert a little piece of RNA into your cells (or rather cells ingest them) and that RNA gets translated into a SARS-CoV-2 spike protein that gets expressed on the surface of the cells and thereby presented to the immune system. So, yes these particular vaccines (although not all) have changed your RNA by adding new RNA to your cells. However, I don’t think this is what the alarmist was worried about. To claim that something that changes is a bad thing implies that the something is fixed and stable to start with, which is profoundly untrue about RNA.

The central dogma of molecular biology is that genetic information flows from DNA to RNA to proteins. All of your genetic material starts as DNA organized in 23 pairs of chromosomes. Your cells will under various conditions transcribe this DNA into RNA, which is then translated into proteins. The biological machinery that does all of this is extremely complex and not fully understood and part of my research is trying to understand this better. What we do know is that transcription is an extremely noisy and imprecise process at all levels. The molecular steps that transcribe DNA to RNA are stochastic. High resolution images of genes in the process of transcription show that transcription occurs in random bursts. RNA is very short-lived, lasting between minutes to at most a few days. There is machinery in the cell dedicated to degrading RNA. RNA is spliced; it is cut up into pieces and reassembled all the time and this splicing happens more or less randomly. Less than 2% of your DNA codes for proteins but virtually all of the DNA including noncoding parts are continuously being transcribed into small RNA fragments. Your cell is constantly littered with random stray pieces of RNA, and only a small fraction of it gets translated into proteins. Your RNA changes. All. The. Time.

Now, a more plausible alarmist statement (although still untrue) would be to say that vaccines change your DNA, which could be a bad thing. Cancer after all involves DNA mutations. There are viruses (retroviruses) that insert a copy of its RNA code into the host’s DNA. HIV does this for example. In fact, a substantial fraction of the human genome is comprised of viral genetic material. Changing proteins can also be very bad. Prion diseases are basically due to misfolded proteins. So DNA changing is not good, protein changing is not good, but RNA changing? Nothing to see here.

COVID, COVID, COVID

Even though Covid- is going to be with us forever, I actually think on the whole the pandemic turned out better than expected, and I mean that in the technical sense. If we were to rerun the pandemic over and over again, I think our universe will end up with fewer deaths than average. That is not to say we haven’t done anything wrong. We’ve botched up many things of course but given that the human default state is incompetence, we botched less than we could have.

The main mistake in my opinion was the rhetoric on masks in March of 2020. Most of the major Western health agencies recommended against wearing masks at that time because they 1) there was already a shortage of N95 masks for health care workers and 2) they thought that cloth and surgical masks were not effective in keeping one from being infected. Right there is a perfect example of Western solipsism; masks were only thought of as tools for self-protection, rather than as barriers for transmission. If only it was made clear early on that the reason we wear masks is not to protect me from you but to protect you from me. (Although there is evidence that masks do protect the wearer too, see here). This would have changed the rhetoric over masks we are having right now. The anti-maskers would be defending their right to harm others rather than the right to not protect themselves from harm.

The thing we got right was in producing effective vaccines. That was simply astonishing. There had never been a successful mRNA-based drug of any type until the BioNTech and Moderna vaccines. Many things had to go right for the vaccines to work. We needed a genetic sequence (Chinese scientists made it public in January), from that sequence we needed a target (the coronavirus spike protein), we needed to be able to stabilize the spike (research that came out of the NIH vaccine center), we needed to make mRNA less inflammatory (years of work especially at Penn), we needed a way to package that mRNA (work out of MIT), and we needed a sense of urgency to get it done (Western governments). Vaccines don’t always work but we managed to get one in less than a year. So many things had to go right for that to happen. The previous US administration should be taking a victory lap because it was developed under their watch, instead of bashing it.

As I’ve said before, I am skeptical we can predict what will happen next but I am going to predict now that there will not be a variant in the next year that will escape from our current vaccines. We may need booster shots and minor tweaks but the vaccines will continue to work. Part of my belief stems from the work of JC Phillips who argues that the SARS-CoV-2 spike protein is already highly optimized and thus there is not much room for it to change and to become infectious. The virus may mutate to replicate faster within the body but the spike will be relatively stable and thus remain a target for the vaccines. The delta variant wave we’re seeing now is a pandemic of the unvaccinated. I have no idea if those against vaccinations will have a change of heart but at some point everyone will be infected and have some immune protection. (I just hope they approve the vaccine for children before winter). SARS-CoV-2 will continue to circulate just like the way the flu strain from the 1918 pandemic still circulates but it won’t be the danger and menace it is now.

The final stretch

The end of the Covid-19 pandemic is within reach. The vaccines have been a roaring success and former Bell Labs physicist J.C. Phillips predicted it (see here). He argued that the spike protein, which is the business end of the SARS-CoV-2 virus, has been optimized to such a degree in SARS-CoV-2 that even a small perturbation from a vaccine can disrupt it. While the new variants perturb the spike slightly and seem to spread faster, they will not significantly evade the vaccine. However, just because the end is within sight doesn’t mean we should not still be vigilante and not mess this up. Europe has basically scored multiple own goals these past few months with their vaccine rollout (or lack thereof) that is a combination of both gross incompetence and excessive conservatism. The Astra-Zeneca vaccine fiasco was a self-inflicted wound by all parties involved. The vaccine is perfectly fine and any side effects are either not related to the vaccine or of such low probability that it should not be a consideration for halting its use. By artificially slowing vaccine distribution, there is a chance that some new mutation could arise that will evade the vaccine. Europe needs to get its act in gear. The US has steadily ramped up vaccinations and is on course to have all willing adults vaccinated by start of summer. Although there has been a plateauing and even slight rise recently because of relaxation from social distancing in some areas, cases and deaths will drop for good by June everywhere in the US. North America will largely be back to normal by mid-summer. However, it is imperative that we press forward and vaccinate the entire world. We will also all need to get booster shots next fall when we get our flu shots.

Nobel Prize has outlived its usefulness

The Nobel Prize in Physiology was awarded for the discovery of Hepatitis C today. The work is clearly deserving of recognition but this is another case where there were definitely more than three people who played an essential role in the work. I really think that the Nobel Prize should change its rules to allow for more winners. Below is my post when one of the winners of this years prize, Michael Houghton, turned down the Gairdner Award in 2013:

Hepatitis C and the folly of prizes

The scientific world was set slightly aflutter when Michael Houghton turned down the prestigious Gairdner Award for the the discovery of Hepatitis C. Harvey Alter and Daniel Bradley were the two other recipients. Houghton, who had previously received the Lasker Award with Alter, felt he could not accept one more award because two colleagues Qui-Lim Choo and George Kuo did not receive either of these awards, even though their contributions were equally important.

Hepatitis, which literally means inflammation of the liver, was characterized by Hippocrates and known to be infectious since the 8th century. The disease had been postulated to be viral at the beginning of the 20th century and by the 1960’s two viruses termed Hepatitis A and Hepatitis B had been established. However, there still seemed to be another unidentified infectious agent which was termed Non-A Non-B Hepatitis NANBH.

Michael Hougton, George Kuo and Qui-Lim Choo were all working at the Chiron corporation in the early 1980’s.   Houghton started a project to discover the cause of NANBH in 1982 with Choo joining a short time later. They made significant process in generating mouse monoclonal antibodies with some specificity to NANBH infected materials from chimpanzee samples received from Daniel Bradley at the CDC. They used the antibodies to screen cDNA libraries from infected materials but they had not isolated an agent. George Kuo had his own lab at Chiron working on other projects but would interact with Houghton and Choo. Kuo suggested that they try blind cDNA immunoscreening on serum derived from actual NANBH patients. This approach was felt to be too risky but Kuo made a quantitative assessment that showed it was viable. After two years of intensive and heroic screening by the three of them, they identified one clone that was clearly derived from the NANBH genome and not from human or chimp DNA. This was definitive proof that NANBH was a virus, which is now called Hepatitis C. Kuo then developed a prototype of a clinical Hepatitis C antibody detection kit and used it to screen a panel of NANBH blood provided by Harvey Alter of the NIH. Kuo’s test was a resounding success and the blood test that came out of that work has probably saved 300 million or more people from Hepititis C infection.

The question then is who deserves the prizes. Is it Bradley and Alter, who did careful and diligent work obtaining samples or is it Houghton, Choo, and Kuo, who did the heroic experiments that isolated the virus? For completely unknown reasons, the Lasker was awarded to just Houghton and Alter, which primed the pump for more prizes to these two. Now that the Lasker and Gairdner prizes have been cleared, that leaves just the Nobel Prize. The scientific community could get it right this time and award it to Kuo, Choo, and Houghton.

Addendum added 2013-5-2:  I should add that many labs from around the world were also trying to isolate the infective agent of NANBH and all failed to identify the correct samples from Alter’s panel.  It is not clear how long it would have been and how many more people would have been infected if Kuo, Choo, and Houghton had not succeeded when they did.

ICCAI talk

I gave a talk at the International Conference on Complex Acute Illness (ICCAI) with the title Forecasting COVID-19. I talked about some recent work with FDA collaborators on scoring a large number of publicly available epidemic COVID-19 projection models and show that they are unable to reliably forecast COVID-19 beyond a few weeks. The slides are here.

Why it is so hard to forecast COVID-19

I’ve been actively engaged in trying to model the COVID-19 pandemic since April and after 5 months I am pretty confident that models can estimate what is happening at this moment such as the number of people who are currently infected but not counted as a case. Back at the end of April our model predicted that the case ascertainment ratio ( total cases/total infected) was on the order of 1 in 10 that varied drastically between regions and that number has gone up with the advent of more testing so that it may now be on the order of 1 in 4 or possibly higher in some regions. These numbers more or less the anti-body test data.

However, I do not really trust my model to forecast what will happen a month from now much less six months. There are several reasons. One is that while the pandemic is global the dynamics are local and it is difficult if not impossible to get enough data for a detailed fine grained model that captures all the interactions between people. Another is that the data we do have is not completely reliable. Different regions define cases and deaths differently. There is no universally accepted definition for what constitutes a case or a death and the definition can change over time even for the same region. Thus, differences in death rates between regions or months could be due to differences in the biology of the virus, medical care, or how deaths are defined and when they are recorded. Depending on the region or time, a person with a SARS-CoV-2 infection who dies of a cardiac arrest may or may not be counted as a COVID-19 death. Deaths are sometimes not officially recorded for a week or two, particularly if the physician is overwhelmed with cases.

However, the most important reason models have difficulty forecasting the future is that modeling COVID-19 is as much if not more about modeling the behavior of people and government policy than modeling the biology of disease transmission and we are just not very good at predicting what people will do. This was pointed out by economist John Cochrane months ago, which I blogged about (see here). You can see why getting behavior correct is crucial to modeling a pandemic from the classic SIR model

where and are the infected and susceptible fractions of the initial population, respectively. Behavior greatly affects the rate of infection and small errors in amplify exponentially. Suppression and mitigation measures such as social distancing, mask wearing, and vaccines reduce , while super-spreading events increase . The amplification of error is readily apparent near the onset of the pandemic where grows like . If you change by , then the will grow like and thus the ratio is growing (or decaying) exponentially like . The infection rate also appears in the initial reproduction number . From a previous post, I derived approximate expressions for how long a pandemic would last and show that it scales as and thus errors in will produce errors , which could result in errors in how long the pandemic will last, which could be very large if is near one.

The infection rate is different everywhere and constantly changing and while it may be possible to get an estimate of it from the existing data there is no guarantee that previous trends can be extrapolated into the future. So while some of the COVID-19 models do a pretty good job at forecasting out a month or even 6 weeks (e.g. see here), I doubt any will be able to give us a good sense of what things will be like in January.

There is no herd immunity

In order for an infectious disease (e.g. COVID-19) to spread, the infectious agent (e.g. SARS-CoV-2) must jump from one person to another. The rate of this happening depends on the rate that an infectious person will come into contact with a susceptible person multiplied by the rate of the virus making the jump when the two people are nearby. The reproduction number R is obtained from the rate of infection spread times the length of time a person is infectious. If R is above one then a single person will infect more than one person on average and thus the pandemic will grow. If it is below one, then the pandemic will diminish. Herd immunity happens when enough people have been infected that the rate of finding a susceptible person becomes low enough that R drops below one. You can find the math behind this here.

However, a major assumption behind herd immunity is that once a person is infected they can never be infected again and this is not true for many infectious diseases such as other corona-viruses and the flu. There are reports that people can be reinfected by SARS-CoV-2. This is not fully validated but my money is on there being no lasting immunity to SARS-CoV-2 and this means that there is never any herd immunity. COVID-19 will just wax and wane forever.

This doesn’t necessarily mean it will be deadly forever. In all likelihood, each time you are infected your immune response will be more measured and perhaps SARS-CoV-2 will eventually be no worse than the common cold or the seasonal flu. But the fatality rate for first time infection will still be high, especially for the elderly and vulnerable. Those people will need to remain vigilante until there is a vaccine, and there is still no guarantee that a vaccine will work in the field. If we’re lucky and we get a working vaccine, it is likely that vaccine will not have lasting effect and just like the flu we will need to be vaccinated annually or even semi-annually.

Another Covid-19 plateau

The world seems to be in another Covid-19 plateau for new cases. The nations leading the last surge, namely the US, Russia, India, and Brazil are now stabilizing or declining, while some regions in Europe and in particular Spain are trending back up. If the pattern repeats, we will be in this new plateau for a month or two and then trend back up again, just in time for flu season to begin.

Why we need a national response

It seems quite clear now that we do not do a very good job of projecting COVID-19 progression. There are many reasons. One is that it is hard to predict how people and governments will behave. A fraction of the population will practice social distancing and withdraw from usual activity in the absence of any governmental mandates, another fraction will not do anything different no matter any official policy and the rest are in between. I for one get more scared of this thing the more I learn about it. Who knows what the long term consequences will be particularly for autoimmune diseases. The virus is triggering a massive immune response everywhere in the body and it could easily develop a memory response to your own cells in addition to the virus.

The virus also spreads in local clusters that may reach local saturation before infecting new clusters but the cross-cluster transmission events are low probability and hard to detect. The virus reached American shores in early January and maybe even earlier but most of those early events died out. This is because the transmission rate is highly varied. A mean reproduction number of 3 could mean everyone has R=3 or that most people transmit with R less than 1 while a small number (or events) transmit with very high R. (Nassim Nicholas Taleb has written copiously on the hazards of highly variable (fat tailed) distributions. For those with mathematical backgrounds, I highly recommend reading his technical volumes: The Technical Incerto. Even if you don’t believe most of what he says, you can still learn a lot.) Thus it is hard to predict when an event will start a local epidemic, although large gatherings of people (i.e. weddings, conventions, etc.) are a good place to start. Once the epidemic starts, it grows exponentially and then starts to saturate either by running out of people in the locality to infect or people changing their behavior or more likely both. Parts of New York may be above the herd immunity threshold now.

Thus at this point, I think we need to take a page out of Taleb’s book (like literally as my daughter would say), and don’t worry too much about forecasting. We can use it as a guide but we have enough information to know that most people are susceptible, about a third will be asymptomatic if infected (which doesn’t mean they won’t have long term consequences), about a fifth to a tenth will be counted as a case, and a few percent of those will die, which strongly depends on age and pre-existing conditions. We can wait around for a vaccine or herd immunity and in the process let many more people die, ( I don’t know how many but I do know that total number of deaths is a nondecreasing quantity), or we can act now everywhere to shut this down and impose a strict quarantine on anyone entering the country until they have been tested negative 3 times with a high specificity PCR test (and maybe 8 out of 17 times with a low specificity and sensitivity antigen test).

Acting now everywhere means, either 1) shutting everything down for at least two weeks. No Amazon or Grubhub or Doordash deliveries, no going to Costco and Walmart, not even going to the super market. It means paying everyone in the country without an income some substantial fraction of their salary. It means distributing two weeks supply of food to everyone. It means truly essential workers, like people keeping electricity going and hospital workers, live in a quarantine bubble hotel, like the NBA and NHL or 2) Testing everyone everyday who wants to leave their house and paying them to quarantine at home or in a hotel if they test positive. Both plans require national coordination and a lot of effort. The CARES act package has run out and we are heading for economic disaster while the pandemic rages on. As a recent president once said, “What have you got to lose?”

The battle over academic freedom

In the wake of George Floyd’s death, almost all of institutional America put out official statements decrying racism and some universities initiated policies governing allowable speech and research. This was followed by the expected dissent from those who worry that academic freedom is being suppressed (see here, here, and here for some examples). Then there is the (in)famous Harper’s Magazine open letter decrying Cancel Culture, which triggered a flurry of counter responses (e.g. see here and here).

While some faculty members in the humanities and (non-life) sciences are up in arms over the thought of a committee of their peers judging what should be allowable research, I do wish to point out that their colleagues over on the Medical campus have had to get approval for human and animal research for decades. Research on human subjects must first pass through an Institutional Review Board (IRB) while animal experiments must clear the Institutional Animal Care and Use Committee (IACUC). These panels ensure that the proposed work is ethical, sound, and justified. Even research that is completely noninvasive, such as analysis of genetic data, must pass scrutiny to ensure the data is not misused and subject identies are strongly protected. Almost all faculty members would agree that this step is important and necessary. History is rife of questionable research that range from careless to criminal. Is it so unreasonable to extend such a concept to the rest of campus?

How to make a fast but bad COVID-19 test good

Among the myriad of problems we are having with the COVID-19 pandemic, faster testing is one we could actually improve. The standard test for the presence of SARS-CoV-2 virus uses PCR (polymerase chain reaction), which amplifies targeted viral RNA. It is accurate (high specificity) but requires relatively expensive equipment and reagents that are currently in short supply. There are reports of wait times of over a week, which renders a test useless for contact tracing.

An alternative to PCR is an antigen test that tests for the presence of protein fragments associated with COVID-19. These tests can in principle be very cheap and fast, and could even be administered on paper strips. They are generally much more unreliable than PCR and thus have not been widely adopted. However, as I show below by applying the test multiple times, the noise can be suppressed and a poor test can be made arbitrarily good.

The performance of binary tests are usually gauged by two quantities – sensitivity and specificity. Sensitivity is the probability that you test positive (i.e are infected) given that you actually are positive (true positive rate). Specificity is the probability that you test negative if you actually are negative (true negative rate). For a pandemic, sensitivity is more important than specificity because missing someone who is infected means you could put lots of people at risk while a false positive just means the person falsely testing positive is inconvenienced (provided they cooperatively self-isolate). Current PCR tests have very high specificity but relatively low sensitivity (as low as 0.7) and since we don’t have enough capability to retest, a lot of tested infected people could be escaping detection.

The way to make any test have arbitrarily high sensitivity and specificity is to apply it multiple times and take some sort of average. However, you want to do this with the fewest number of applications. Suppose we administer tests on the same subject, the probability of getting more than positive tests if the person is positive is , where is the cumulative distribution function of the Binomial distribution (i.e. probability that the number of Binomial distributed events is less than or equal to ). If the person is negative then the probability of  or fewer positives is . We thus want to find the minimal given a desired sensitivity and specificity, and . This means that we need to solve the constrained optimization problem: find the minimal under the constraint that , and . decreases and increases with increasing and vice versa for . We can easily solve this problem by sequentially increasing and scanning through until the two constraints are met. I’ve included the Julia code to do this below.  For example, starting with a test with sensitivity .7 and specificity 1 (like a PCR test), you can create a new test with greater than .95 sensitivity and specificity, by administering the test 3 times and looking for a single positive test. However, if the specificity drops to .7 then you would need to find more than 8 positives out of 17 applications to be 95% sure you have COVID-19.

 

using Distributions

function Q(k,n,q)
d = Binomial(n,q)
return 1 – cdf(d,k)
end

function R(k,n,r)
d = Binomial(n,1-r)
return cdf(d,k)
end

function optimizetest(q,r,qp=.95,rp=.95)

nout = 0
kout = 0

for n in 1:100
for k in 0:n-1
println(R(k,n,r),” “,Q(k,n,q))
if R(k,n,r) >= rp && Q(k,n,q) >= qp
kout=k
nout=n
break
end
end
if nout > 0
break
end
end

return nout, kout
end

Slides for Covid-19 talk

Here are my slides for my recent COVID-19 talk at the Centre for Applied Mathematics in BioScience and Medicine (CAMBAM). It’s an updated version of the one I gave to the FDA.

Remember the ventilator

According to our model, the global death rate due to Covid-19 is around 1 percent for all infected (including unreported). However, if it were not for modern medicine and in particular the ventilator, the death rate would be much higher. Additionally, the pandemic first raged in the developed world and is only recently engulfing parts of the world where medical care is not as ubiquitous although this may be mitigated by a younger populace in those places. The delay between the appearance of a Covid-19 case and deaths is also fairly long; our model predicts a mean of over 50 days. So the lower US death rate compared to April could change in a month or two when the effects of the recent surges in the US south and west are finally felt.

How long and how high for Covid-19

Cases of Covid-19 are trending back up globally and in the US. The world has nearly reached 10 million cases with over 2.3 million in the US. There is still a lot we don’t understand about SARS-CoV-2 transmission but I am confident we are no where near herd immunity. Our model is consistently showing that the case ascertainment ratio, that is the ratio of official Covid-19 cases to total SARS-CoV-2 infections, is between 5 and 10. That means that the US has less than 25 million infections while the world is less than 100 million.

Herd immunity means that for any fixed reproduction number, R0, the number of active infections will trend downward if the fraction of the initially susceptible population falls below 1/R0, or the total number infected is higher than 1- 1/R0. Thus, for an R0 of 4, three quarters of the population needs to be infected to reach herd immunity. However, the total number that will eventually be infected, as I will show below, will be

which is considerably higher. Thus, mitigation efforts to reduce R0 will reduce the total number infected. (2020-06-27: This expression is not accurate when R0 is near 1. For a formula in that regime, see Addendum.)

Some regions in Western Europe, East Asia, and even the US have managed to suppress R0 below 1 and cases are trending downward. In the absence of reintroduction of SARS-CoV-2 carriers, Covid-19 can be eliminated in these regions. However, as the recent spikes in China, South Korea, and Australia have shown, this requires continual vigilance. As long as any person remains infected in the world, there is always a chance of re-emergence. As long as new cases are increasing or plateauing, R0 remains above 1. As I mentioned before, plateauing is not a natural feature of the epidemic prediction models, which generally either go up or go down. Plateauing requires either continuous adjustment of R0 through feedback or propagation through the population as a wave front, like a lawn mower cutting grass. The latter is what is actually going on from what we are seeing. Regions seem to rise and fall in succession. As one region reaches a peak and goes down either through mitigation or rapid spread of SARS-CoV-2, Covid-19 takes hold in another. We saw China and East Asia rise and fall, then Italy, then the rest of Western Europe, then New York and New Jersey, and so forth in series, not in parallel. Now it is spreading throughout the rest of the USA, South America, and Eastern Europe. Africa has been spared so far but it is probably next as it is beginning to explode in South Africa.

A reduction in R0 also delays the time to reach the peak. As a simple example, consider the standard SIR model

where is the fraction of the population susceptible to SARS-CoV-2 infection and is the fraction of the population actively infectious. Below are simulations of the pandemic progression for R0 = 4 and 2.

We see that halving R0, basically doubles the time to reach the peak but much more than doubles the number of people that never get infected. We can see why this is true by analyzing the equations. Dividing the two SIR equations gives

,

which integrates to . If we suppose that initially and then we get

(*)

where is the reproduction number. The total number infected will be for . Rearranging gives

If we assume that and ignore we can expand the exponential and solve for to get

This is the fraction of the population that never gets infected, which is also the probability that you won’t be infected. It gets smaller as increases. So reducing can exponentially reduce your chances of being infected.

To figure out how long it takes to reach the peak, we substitute equation (*) into the SIR equation for to get

We compute the time to peak, , by separating variables and integrating both sides. The peak is reached when .  We must thus compute

We can’t do this integral but if we set and , then we can expand and obtain

where . This can be re-expressed as

which is integrated to

If we assume that , then we get an expression

So, is proportional to the recovery time and inversely related to as expected but if is very small (say 0.00001) compared to (say 3) then can be big (around 10), which may explain why it takes so long for the pandemic to get started in a region. If the infection rate is very low in a region, the time it takes a for a super-spreader event to make an impact could be much longer than expected (10 times the infection clearance time (which could be two weeks or more)).

 

Addendum 2020-06-26: Fixed typos in equations and added clarifying text to last paragraph

 

Addendum 2020-06-27: The approximation for total infected is not very good when is near 1, a better one can be obtained by expanding the exponential to quadratic order in which case you get the new formula for the

However, for near 1, a better expansion is to substitute into equation (*) and obtain

Set , after rearranging and exponentiating,  obtain

, which can be expanded to yield

Solving for gives the total fraction infected to be

This took me much longer than it should have.

 

The fatal flaw of the American Covid-19 response

The United States has surpassed 2 million official Covid-19 cases and a 115 thousand deaths. After three months of lockdown, the country has had enough and is reopening. Although it has achieved its initial goal of slowing the growth of the pandemic so that hospitals would not be overwhelmed, the battle has not been won. We’re not at the beginning of the end; we may not even be at the end of the beginning. If everyone in the world could go into complete isolation, the pandemic would be over in two weeks. Instead, it is passed from one person to the next in a tragic relay race. As long as a single person is shedding the SARS-CoV-2 virus and comes in contact with another person, the pandemic will continue. The pandemic in the US is not heading for extinction. We are not near herd immunity and R0 is not below one. By the most optimistic yet plausible scenario, 30 million people have already been infected and 200 million will never get it either by having some innate immunity or by avoiding it through sheltering or luck. However, that still leaves over 100 million who are susceptible of which about a million will die if they all catch it.

However, the lack of effectiveness of the response is not the fatal flaw. No, the fatal flaw is that the US Covid-19 response asks one set of citizens to sacrifice for the benefit of another set. The Covid-19 pandemic is a story of three groups of people. The fortunate third can work from home, and the lockdown is mostly just an inconvenience. They still get paychecks while supplies and food can be delivered to their homes. Sure it has been stressful and many of have forgone essential medical care but they can basically ride this out for as long as it takes. The second group who own or work in shuttered businesses have lost their income. The federal rescue package is keeping some of them afloat but that runs out in August. The choice they have is to reopen and risk getting infected or be hungry and homeless. Finally, the third group is working to allow the first group to remain in their homes. They are working on farms, food processing plants, and grocery stores. They are cutting lawns, fixing leaking pipes, and delivering goods. They are working in hospitals and nursing homes and taking care of the sick and the children of those who must work. They are also the ones who are most likely to get infected and spread it to their families or the people they are trying to take care of. They are dying so others may live.

A lockdown can only work in a society if the essential workers are adequately protected and those without incomes are supported. Each worker should have an N100 mask, be trained how to wear it and be tested weekly. People in nursing homes should be wearing hazmat suits. Everyone who loses income should be fully compensated. In a fair society, everyone should share the risks and the pain equally.