Action on a whim

September 29, 2011 Carson Chow Evolution, Genetics, Neuroscience, Uncategorized

One of the big news stories last week was the publication in Science on the genomic sequence of a hundred year old Aboriginal Australian. The analysis finds that the Aboriginal Australians are descendants of an early migration to Asia between 62,000 and 75,000 years ago and this migration is different from the one that gave rise to modern Asians 25,000 to 38,000 years ago. I have often been amazed that humans were able to traverse over harsh terrain and open water into the complete unknown. However, I briefly watched a documentary on CNBC last night about Apocalypse 2012 that made me understand this much better. Evidently, there is a fairly large group of people who believe the world will end in 2012. (This is independent of the group that thought the world would end earlier this year.) The prediction is based on the fact that a large cycle in the Mayan calendar will supposedly end in 2012. According to some of the believers, the earth’s rotation will reverse and that will cause massive earthquakes and tsunamis. These believers have thus managed to recruit followers and start building colonies in the mountains to try to survive. People are taking this extremely seriously. I think this ability to change the course of one’s entire life on the flimsiest of evidence is what led our ancestors to leave Africa and head into the unknown. People will get ideas in their head and nothing will stop them from pursuing them. It’s what led us to populate every corner of the world and reshape much of the surface of the earth. It also suggests that the best optimization algorithms that seek a global maximum may be ones that have some ‘momentum’ so that they can leave local maxima and head downhill to find higher peaks elsewhere.

Infinite growth on finite resources

September 23, 2011September 23, 2011 Carson Chow Economics, Environment, Technology

At this past summer’s Lindau meeting of Nobel Laureates, Christian Rene de Duve, who is over 90 years old, gave a talk on population growth and its potential dire effects on the world. Part of his talk was broadcast on the Science Show. His talk prompted me to think more about growth. The problem is not that the population is growing per se. Even if the population were stable, we would still eventually run out of fossil fuels if we consume energy at the same rate. The crucial thing is that we must progressively get more efficient. For example, consider a steady population where we consume some finite resource at the rate of $t^\alpha$ . Then so long as $\alpha < -1$ , we can make that resource last forever since $\int_1^\infty t^\alpha$ is finite. Now, if the population is growing exponentially then we would have to become exponentially more efficient with time to make the resource last. However, making the world more efficient will take good ideas and skilled people to execute them and that will scale with the population. So there might be some optimal growth rate where we ensure the idea generation rate is sufficient to increase efficiency so that we can sustain forever.

Globalization and income distribution

September 18, 2011 Carson Chow Economics, Pedagogy

In the past two decades we have seen both an increase in globalization and income inequality. The question is whether the two are directly or indirectly related. The GDP of the United States is about 14 trillion dollars, which works out to be about 45 thousand per person. However, the median household income, which is about 50 thousand dollars per household, has not increased over this time period and has even dropped a little this year. The world GDP is approximately 75 trillion dollars (in terms of purchase power parity), which is an amazingly high 11 thousand per person per year given that over a billion people live on under two dollars a day. Thus one way to explain the decline in median income is that the US worker is now competing in a world where per capita GDP has effectively been reduced by a factor of four. However, does this also explain the concurrent increase in wealth at the top of the income distribution.

I thought I would address this question with an extremely simple income distribution model called the Pareto distribution. It simply assumes that incomes are distributed according to a power law with a lower cutoff: $P(I) = \alpha A I^{-1-\alpha}$ , for $I>L$ , where $A$ is a normalization constant. Let’s say the population size is $N$ and the GDP is $G$ . Hence, we have the conditions $\int_L^\infty P(I) dI = N$ and $\int_L^\infty IP(I) dI = G$ . Inserting the Pareto distribution gives the following conditions $N=AL^{-\alpha}$ and $G = \alpha N L/(1-\alpha)$ , or $A = NL^\alpha$ and $L=(\alpha-1)/\alpha (G/N)$ . The Pareto distribution is thought to be valid mostly for the tail fo the income distribution so $L$ should only be thought of as an effective minimum income. We can now calculate the income threshold for the top 1% say. This is given by the condition $F(H) = N-\int_L^H P(I) dI = 0.01N$ , which results in $(L/H)^\alpha=0.01$ or $H = L/0.01^{1/\alpha}$ . For $\alpha = 2$ then the 99 percentile income threshold is about two hundred thousand dollars, which is a little low, implying that $\alpha$ is less than two. However, the crucial point is that $H$ scales with the average income $G/N$ . The median income would have the same scaling, which clearly goes against recent trends where median incomes have stagnated while top incomes have soared. What this implies is that the top end obeys a different income distribution from the rest of us.

Correlations

September 10, 2011September 10, 2011 Carson Chow Economics, Opinion, Pedagogy, Statistics

If I had to compress everything that ails us today into one word it would be correlations. Basically, everything bad that has happened recently from the financial crisis to political gridlock is due to undesired correlations. That is not to say that all correlations are bad. Obviously, a system without any correlations is simply noise. You would certainly want the activity on an assembly line in a factory to be correlated. Useful correlations are usually serial in nature like an invention leads to a new company. Bad correlations are mostly parallel like all the members in Congress voting exclusively along party lines, which reduces an assembly with hundreds of people into just two. A recession is caused when everyone in the economy suddenly decides to decrease spending all at once. In a healthy economy, people would be uncorrelated so some would spend more when others spend less and the aggregate demand would be about constant. When people’s spending habits are tightly correlated and everyone decides to save more at the same time then there would be less demand for goods and services in the economy so companies must lay people off resulting in even less demand leading to a vicious cycle.

The financial crisis that triggered the recession was due to the collapse of the housing bubble, another unwanted correlated event. This was exacerbated by collateralized debt obligations (CDOs), which are financial instruments that were doomed by unwanted correlations. In case you haven’t followed the crisis, here’s a simple explanation. Say you have a set of loans where you think the default rate is 50%. Hence, given a hundred mortgages, you know fifty will fail but you don’t know which. The way to make a triple A bond out of these risky mortgages is to lump them together and divide the lump into tranches that have different seniority (i.e. get paid off sequentially). So the most senior tranche will be paid off first and have the highest bond rating. If fifty of the hundred loans go bad, the senior tranche will still get paid. This is great as long as the mortgages are only weakly correlated and you know what that correlation is. However, if the mortgages fail together then all the tranches will be bad. This is what happened when the bubble collapsed. Correlations in how people responded to the collapse made it even worse. When some CDOs started to fail, people panicked collectively and didn’t trust any CDOs even though some of them were still okay. The market for CDOs became frozen so people who had them and wanted to sell them couldn’t even at a discount. This is why the federal government stepped in. The bail out was deemed necessary because of bad correlations. Just between you and me, I would have let all the banks just fail.

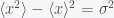We can quantify the effect of correlations in a simple example, which will also show the difference between sample mean and population mean. Let’s say you have some variable $x$ that estimates some quantity. The expectation value (population mean) is $\langle x \rangle = \mu$ . The variance of $x$ , $\langle x^2 \rangle - \langle x \rangle^2=\sigma^2$ gives an estimate of the square of the error. If you wanted to decrease the error of the estimate then you can take more measurements. So let’s consider a sample of 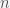$n$ measurements. The sample mean is 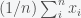$(1/n)\sum_i^n x_i$ . The expectation value of the sample mean is $(1/n)\sum_i \langle x_i \rangle = (n/n)\langle x \rangle = \mu$ . The variance of the sample mean is

$\langle [(1/n)\sum_i x_i]^2 \rangle - \langle x \rangle ^2 = (1/n^2)\sum_i \langle x_i^2\rangle + (1/n^2) \sum_{j\ne k} \langle x_j x_k \rangle - \langle x \rangle^2$

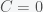Let $C=\langle (x_j-\mu)(x_k-\mu)\rangle$ be the correlation between two measurements. Hence, $\langle x_j x_k \rangle = C +\mu^2$ . The variance of the sample mean is thus $\frac{1}{n} \sigma^2 + \frac{n-1}{n} C$ . If the measurements are uncorrelated ( $C=0$ ) then the variance is 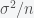$\sigma^2/n$ , i.e. the standard deviation or error is decreased by the square root of the number of samples. However, if there are nonzero correlations then the error can only be reduced to the amount of correlations $C$ . Thus, correlations give a lower bound in the error on any estimate. Another way to think about this is that correlations reduce entropy and entropy reduces information. One way to cure our current problems is to destroy parallel correlations.

Computability

September 2, 2011September 2, 2011 Carson Chow Computer Science, Mathematics, Pedagogy, Philosophy

Many of my recent posts centre around the concept of computability so I thought I would step back today and give a review of the topic for the uninitiated. Obviously, there are multiple text books on the topic so I won’t be bringing anything new. However, I would like to focus on one small aspect of it that is generally glossed over in books. The main thing to take away from computability for me is that it involves functions of integers. Essentially, a computation is something that maps an integer to another integer. The Church-Turing thesis states that all forms of computation are equivalent to a Turing machine. Hence, the lambda calculus, certain cellular automata, and your MacBook have the same computational capabilities as a Turing machine (actually your MacBook is finite so it has less capability but it could be extended arbitrarily to be Turing complete). The thesis cannot be formally proven but it seems to hold.

The fact that computation is about manipulation of integers has profound consequences, the main one being that it cannot deal directly with real numbers. Or to put it another way, computation is constrained to countable processes. If anything requires an uncountable number of operations then it is uncomputable. However, uncomputability or undecidability as it is often called, is generally not presented in such a simple way. In many popular books like Godel, Escher, Bach, the emphasis is on the magical aspect of it. The reason is that the proof on uncomputability, which is similar to Godel’s proof of the First Incompleteness Theorem, relies on demonstrating that a certain self-referential function or program cannot exist by use of Cantor’s diagonal slash argument that the reals are uncountable. In very simple nonrigorous terms, the proof works by considering a list of all possible computable functions $f_i(j)$ on all the integers $j$ . This is the same as saying you have a list of all possible Turing machines $i$ , of all possible initial states $j$ . Now you suppose that one of the functions $f_a(j)$ takes the output of function j given input $j$ and puts a negative sign in front. So $f_a(j)= -f_j(j)$ . The problem then comes if you suppose that the function acts on itself because then $f_a(a)=-f_a(a)$ , which is a contradiction and thus such a computable function $f_a$ cannot exist.