Falling through the earth

The 2012 remake of the classic film Total Recall features a giant elevator that plunges through the earth from Australia to England. This trip is called the “fall”, which I presume to mean it is propelled by gravity alone in an evacuated tube. The film states that the trip takes 17 minutes (I don’t remember if this is to get to the center of the earth or the other side). It also made some goofy point that the seats flip around in the vehicle when you cross the center because gravity reverses. This makes no sense because when you fall you are weightless and if you are strapped in, what difference does it make what direction you are in. In any case, I was still curious to know if 17 minutes was remotely accurate and the privilege of a physics education is that one is given the tools to calculate the transit time through the earth due to gravity.

The first thing to do is to make an order of magnitude estimate to see if the time is even in the ballpark. For this you only need middle school physics. The gravitational acceleration for a mass at the surface of the earth is . The radius of the earth is 6.371 million metres. Using the formula that distance (which you get by integrating twice over time), you get . Plugging in the numbers gives 1140 seconds or 19 minutes. So it would take 19 minutes to get to the center of the earth if you constantly accelerated at . It would take the same amount of time to get back to the surface. Given that the gravitational acceleration at the surface should be an upper bound, the real transit time should be slower. I don’t know who they consulted but 17 minutes is not too far off.

We can calculate a more accurate time by including the effect of the gravitational force changing as you transit through the earth but this will require calculus. It’s a beautiful calculation so I’ll show it here. Newton’s law for the gravitational force between a point mass m and a point mass M separated by a distance r is

where is the gravitational constant. If we assume that mass M (i.e. earth) is fixed then Newton’s 2nd law of motion for the mass m is given by . The equivalence of inertial mass and gravitational mass means you can divide m from both sides. So, if a mass m were outside of the earth, then it would accelerate towards the earth as

and this number is g when r is the radius of the earth. This is the reason that all objects fall with the same acceleration, apocryphally validated by Galileo on the Tower of Pisa. (It is also the basis of the theory of general relativity).

However, the earth is not a point but an extended ball where each point of the ball exerts a gravitational force on any mass inside or outside of the ball. (Nothing can shield gravity). Thus to compute the force acting on a particle we need to integrate over the contributions of each point inside the earth. Assume that the density of the earth is constant so the mass where is the radius of the earth. The force between two point particles acts in a straight line between the two points. Thus for an extended object like the earth, each point in it will exert a force on a given particle in a different direction. So the calculation involves integrating over vectors. This is greatly simplified because a ball is highly symmetric. Consider the figure below, which is a cross section of the earth sliced down the middle.

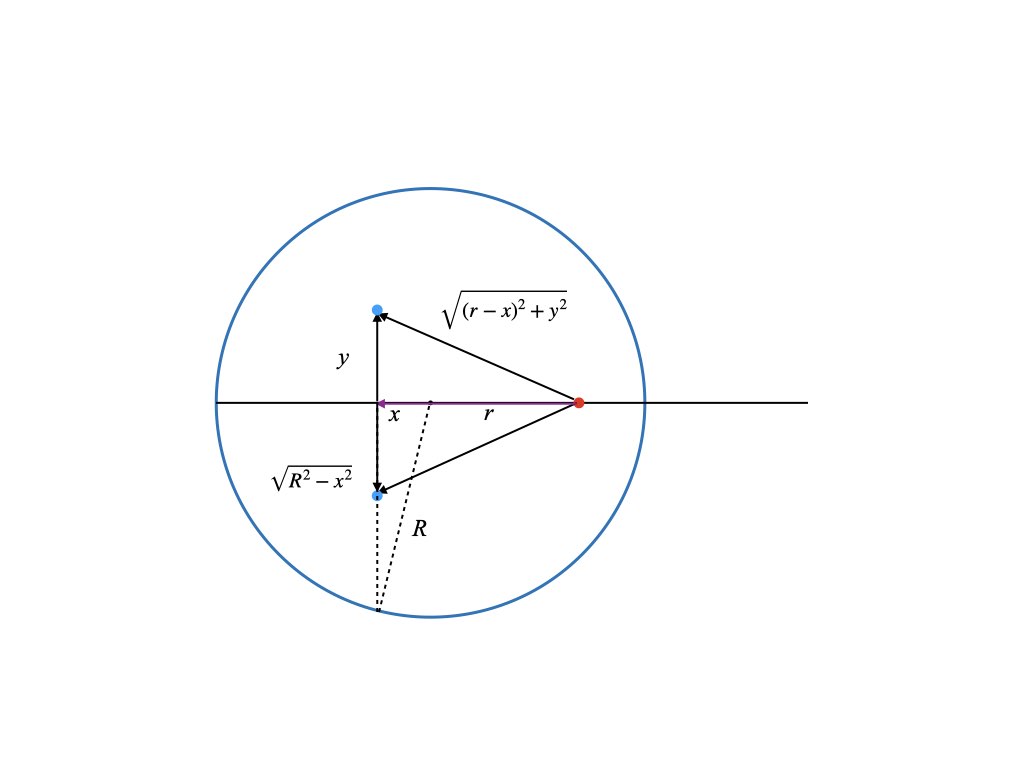
The particle/elevator is the red dot, which is located a distance r from the center. (It can be inside or outside of the earth). We will assume that it travels on an axis through the center of the earth. We want to compute the net gravitational force on it from each point in the earth along this central axis. All distances (positive and negative) are measured with respect to the center of the earth. The blue dot is a point inside the earth with coordinates (x,y). There is also the third coordinate coming out of the page but we will not need it. For each blue point on one side of the earth there is another point diametrically opposed to it. The forces exerted by the two blue points on the red point are symmetrical. Their contributions in the y direction are exactly opposite and cancel leaving the net force only along the x axis. In fact there is an entire circle of points with radius y (orthogonal to the page) around the central axis where each point on the circle combines with a partner point on the opposite side to yield a force only along the x axis. Thus to compute the net force on the elevator we just need to integrate the contribution from concentric rings over the volume earth. This reduces an integral over three dimensions to just two.

The magnitude of the force (density) between the blue and red dot is given by

To get the component of the force along the x direction we need to multiple by the cosine of the angle between the central axis and the blue dot, which is

(i.e. ratio of the adjacent to the hypotenuse of the relevant triangle). Now, to capture the contributions for all the pairs on the circle we multiple by the circumference which is . Putting this together gives

The y integral extends from zero to the edge of the earth, which is . (This is R at (the center) and zero at (the poles) as expected). The x integral extends from one pole to the other, hence -R to R. Completing the y integral gives

(*)

The second term comes from the 0 limit of the integral, which is . The square root of a number has positive and negative roots but the denominator here is a distance and thus is always a positive quantity and thus must include the absolute value. The first term of the above integral can be completed straightforwardly (I’ll leave it as an exercise) but the second term must be handled with care because r-x can change sign depending on whether r is greater or less than x. For a particle outside of the earth r-x is always positive and we get

Inside the earth, we must break the integral up into two parts

The first term of (*) integrates to

Using the fact that , we get

(We again need the absolute value sign). For , the particle is outside of the earth) and . Putting everything together gives

Thus, we have explicitly shown that the gravitational force exerted by a uniform ball is equivalent to concentrating all the mass in the center. This formula is true for too.

For we have

Remarkably, the gravitational force on a particle inside the earth is just the force on the surface scaled by the ratio r/R. The equation of motion of the elevator is thus

with

(Recall that the gravitational acceleration at the surface is ). This is the classic equation for a harmonic oscillator with solutions of the form . Thus, a period (i.e. round trip) is given by . Plugging in the numbers gives 5062 seconds or 84 minutes. A transit through the earth once would be half that at 42 minutes and the time to fall to the center of the earth would be 21 minutes, which I find surprisingly close to the back of the envelope estimate.

Now Australia is not exactly antipodal to England so the tube in the movie did not go directly through the center, which would make the calculation much harder. This would be a shorter distance but the gravitational force would be at an angle to the tube so there would be less acceleration and something would need to keep the elevator from rubbing against the walls (wheels or magnetic levitation). I actually don’t know if it would take a shorter or longer time than going through the center. If you calculate it, please let me know.

The dynamics of inflation

Inflation, the steady increase of prices and wages, is a nice example of what is called a marginal mode, line attractor, or invariant manifold in dynamical systems. What this means is that the dynamical system governing wages and prices has an equilibrium that is not a single point but rather a line or curve in price and wage space. This is easy to see because if we suddenly one day decided that all prices and wages were to be denominated in some other currency, say Scooby Snacks, nothing should change in the economy. Instead of making 15 dollars an hour, you now make 100 Scooby Snacks an hour and a Starbucks Frappuccino will now cost 25 Scooby Snacks, etc. As long as wages and prices are in balance, it does not matter what they are denominated in. That is why the negative effects of inflation are more subtle than simply having everything cost more. In a true inflationary state your inputs should always balance your outputs but at an ever increasing price. Inflation is bad because it changes how you think about the future and that adjustments to the economy always take time and have costs.

This is why our current situation of price increases does not yet constitute inflation. We are currently experiencing a supply shock that has made goods scarce and thus prices have increased to compensate. Inflation will only take place when businesses start to increase prices and wages in anticipation of future increases. We can show this in a very simple mathematical model. Let P represent some average of all prices and W represent average wages (actually they will represent the logarithm of both quantities but that will not matter for the argument). So in equilibrium P = W. Now suppose there is some supply shock and prices now increase. In order to get back into equilibrium wages should increase so we can write this as

where the dot indicates the first derivative (i.e. rate of change of W is positive if P is greater than W). Similarly, if wages are higher than prices, prices should increase and we have

Now notice that the equilibrium (where there is no change in W or P) is given by W=P but given that there is only one equation and two unknowns, there is no unique solution. W and P can have any value as long as they are the same. W – P = 0 describes a line in W-P space and thus it is called a line attractor. (Mathematicians would call this an invariant manifold because a manifold is a smooth surface and the rate of change does not change (i.e. is invariant) on this surface. Physicists would call this a marginal mode because if you were to solve the eigenvalue equation governing this system, it would have a zero eigenvalue, which means that its eigenvector (called a mode) is on the margin between stable and unstable.) Now if you add the two equations together you get

which implies that the rate of change of the sum of P and W, which I call S, is zero. i.e. there is no inflation. Thus if prices and wages respond immediately to changes then there can be no inflation (in this simple model). Now suppose we have instead

The second derivative of W and P respond to differences. This is like having a delay or some momentum. Instead of the rate of S responding to price wage differences, the rate of the momentum of S reacts. Now when we add the two equations together we get

If we integrate this we now get

where C is some nonnegative constant. So in this situation, the rate of change of S is positive and thus S will just keep on increasing forever. Now what is C? Well it is the anticipatory increases in S. If you were lucky enough that C was zero (i.e. no anticipation) then there would be no inflation. Remember that W and P are logarithms so C is the rate of inflation. Interestingly, the way to combat inflation in this simple toy model is to add a first derivative term. This changes the equation to

which is analogous to adding friction to a mechanical system (used differently to what an economist would call friction). The first derivative counters the anticipatory effect of the second derivative. The solution to this equation will return to a state zero inflation (exercise to the reader).

Now of course this model is too simple to actually describe the real economy but I think it gives an intuition to what inflation is and is not.

2022-05-18: Typos corrected.

New Paper on Sars-CoV-2

Phase transitions may explain why SARS-CoV-2 spreads so fast and why new variants are spreading faster

J.C.Phillips, Marcelo A.Moret, Gilney F.Zebende, Carson C.Chow

Abstract

The novel coronavirus SARS CoV-2 responsible for the COVID-19 pandemic and SARS CoV-1 responsible for the SARS epidemic of 2002-2003 share an ancestor yet evolved to have much different transmissibility and global impact ¹. A previously developed thermodynamic model of protein conformations hypothesized that SARS CoV-2 is very close to a new thermodynamic critical point, which makes it highly infectious but also easily displaced by a spike-based vaccine because there is a tradeoff between transmissibility and robustness ². The model identified a small cluster of four key mutations of SARS CoV-2 that predicts much stronger viral attachment and viral spreading compared to SARS CoV-1. Here we apply the model to the SARS-CoV-2 variants Alpha (B.1.1.7), Beta (B.1.351), Gamma (P.1) and Delta (B.1.617.2)³ and predict, using no free parameters, how the new mutations will not diminish the effectiveness of current spike based vaccines and may even further enhance infectiousness by augmenting the binding ability of the virus.

https://www.sciencedirect.com/science/article/pii/S0378437122002576?dgcid=author

This paper is based on the ideas of physicist Jim Phillips, (formerly of Bell Labs, a National Academy member, and a developer of the theory behind Gorilla Glass used in iPhones). It was only due to Jim’s dogged persistence and zeal that I’m even on this paper although the persistence and zeal that ensnared me is the very thing that alienates most everyone else he tries to recruit to his cause.

Jim’s goal is to understand and characterize how a protein will fold and behave dynamically by utilizing an amino acid hydrophobicity (hydropathy) scale developed by Moret and Zebende. People have been developing hydropathy scores for many decades as a way to understand proteins with the idea that hydrophobic amino acids (residues) will tend to be on the inside of proteins while hydrophillic residues will be on the outside where the water is. There are several existing scores but Moret and Zebende, who are physicists and not chemists, took a different tack and found how the solvent-accessible surface area (ASA) scales with the size of a protein fragment with a specific residue in the center. The idea being that the smaller the ASA the more hydrophobic the residue. As protein fragments get larger they will tend to fold back on themselves and thus reduce the ASA. They looked at several thousand protein fragments and computed the average ASA with a given amino acid in the center. When they plotted the ASA vs length of fragment they found a power law and each amino acid had its own exponent. The more negative the exponent the smaller the ASA and thus the more hydrophobic the residue. The (negative) exponent could then be used as a hydropathy score. It differs from other scores in that it is not calculated in isolation based on chemical properties but accounts for the background of the amino acid.

M and Z’s score blew Jim’s mind because power laws are indicative of critical phenomena and phase transitions. Jim computed the coarse-grained hydropathy score (over a window of 35 residues) at each residue of a protein for a number of protein families. When COVID came along he naturally applied it to coronaviruses. He found that the coarse-grained hydropathy score profile of the spike protein of SARS-CoV-1 and SARS-CoV-2 had several deep hydrophobic wells. The well depths were nearly equal with SARS-CoV-2 being more equal than SARS-CoV-1. He then hypothesized that there was a selection advantage for well-depth symmetry and evolutionary pressure had pushed the SARS-CoV-2 spike to be near optimal. He argues that the symmetry allows the protein to coordinate activity better much like the way oscillators synchronize easier if their frequencies are more uniform. He predicted that given this optimality the spike was fragile and thus spike vaccines would be highly effective and that spike mutations could not change the spike much without diminishing function.

My contribution was to write some Julia code to automate this computation and apply it to some SARS-CoV-2 variants. I also scanned window sizes and found that the well depths are most equal close to Jim’s original value of 35. Below is Figure 3 from the paper.

Figure 3.  Hydropathy score Ψ(R,W) for CoV-1, CoV-2, Alpha, and Delta, at the optimal W. The six local hydropathic minima (hydrophilic maxima) are much more symmetric in CoV-2 and variants compared to CoV-1. Minimum 1 is located within the RBD (residues 331-524), which also contains other local minima and maxima.

What you see is the coarse-grained hydropathy score of the spike protein which is a little under 1300 residues long. Between residue 400 and 1200 there are 6 hydropathic wells. The well depths are more similar for SARS-CoV-2 and variants than SARS-CoV-1. Omicron does not look much different from the wild type, which makes me think that Omicron’s increased infectiousness is probably due to mutations that affect viral growth and transmission rather than spike binding to ACE2 receptors.

Jim is encouraging (strong arming) me into pushing this further, which I probably will given that there are still so many unanswered questions as to how and why it works, if at all. If anyone is interested in this, please let me know.