I was invited to write a short profile of my career for DSWeb this week. You can find it here.
The venture capital subsidy is over
Much has been written about the low approval of the current President and the general disgruntlement of the population despite conventional economic measures being good. The unemployment rate is low, wages are rising, and inflation is abating. The most logical explanation is that while the rate of inflation is slowing prices are still higher than before and while unemployment affects a few, high prices affect everyone. I think this is correct but one thing that doesn’t seem to be mentioned is that one of the reasons prices are higher and in some cases much higher is that many of the tech sector services that people relied on like ride share and food delivery were basically giving away their goods for free before and now they are not. Companies like Uber, DoorDash, and Grubhub were never profitable and were kept afloat by unlimited venture capital money, especially from SoftBank, and now this subsidy is gone. Now if you want a ride or get food delivered, you’re going to have to pay full price and this has made a lot of people really unhappy.
The subsidy was premised on the Silicon Valley idea that all start-ups need to “scale” until they are a virtual monopoly (like Amazon, Google/Alphabet and Facebook/Meta). However, the one thing that these tech strategists seemed to not consider is that scaling is useful when getting bigger means getting better, either by having lower cost, acquiring more data, or exploiting network effects. Scaling can work for search and entertainment companies because the more users there are the more data you have to determine what people want. It works for social network companies because the more people there are on the network, the more other people want to join that network. However, it doesn’t really work for delivery and transportation. Costs do not really decrease if Uber or DoorDash get bigger. You still need to pay a person to drive a car and the more miles they drive the more it costs. It could possibly scale if the cars were bigger and drove on fixed routes (like public transportation) but no one has yet to figure out how to scale point-to-point services. The pitch was that the tech companies would optimize the routes but that essentially means solving the “traveling salesman problem” which is NP-complete (i.e. cannot be easily solved and gets exponentially harder as the size gets bigger). Thus, while these tech companies got bigger they just burned through more cash. The primary beneficiaries were us. We got rides and food for next to nothing and now that’s over. However, it was not all costless. It hurt existing industries like traditional taxis, which were heavily regulated. One of the greatest failures in oversight was letting Uber operate in New York but that is another story.
Now these companies are either going bankrupt or increasing their prices. It is true that inflation is partially responsible for ending the subsidy because it led to higher interest rates which made borrowing more expensive but the reckoning would have to come sooner or later. Technological idealism does not obviate the laws of physics or capitalism – all businesses need to make money.
The myth of the zero sum college admission game
A major concern of the commentary in the wake of the recent US Supreme Court decision eliminating the role of race in college admission is how to maintain diversity in elite colleges. What is not being written about is that maybe we shouldn’t have exclusive elite colleges to start with. Americans seem to take for granted that attending an elite college is a zero sum game. However, there is no reason that a so-called elite education must be a scarce resource. Harvard, with its 50 billion plus endowment could easily expand its incoming freshman class by a factor of 5 or 10. It doesn’t because that obviously would make its product less prestigious and diminish its brand. It is a policy decision that allows elite universities like Harvard and Stanford to maintain their status. Being old is not an excuse. Ancient universities in Europe like the University of Bologna in Italy or University of Heidelberg in Germany, are state run and have acceptance rates well over 50%.
The main problem in the US is not that exclusive universities exist but that they have undue power. Kids are scrambling to get in because they believe it gives them a leg up in life. And they are mostly correct. All the Supreme Court Judges, save one, went to either Harvard or Yale law school. The faculty of elite schools tend to get their degrees from elite schools. High power consulting, Wall Street, and law firms tend to recruit from a small set of elite schools. Yet, this is only because we as a society choose it to be this way. In the distant past, elite colleges were basically finishing schools for the wealthy and powerful. Going to an Ivy league school was not what conferred you power and wealth. You were there because you already had power and wealth. It has only been in the past half century or so that the elite schools started admitting on the basis of merit. The cynical view is that world was getting more technical and thus it was useful for the wealthy and powerful to have access to talented recruits.
While it is true that the top schools generally have more resources and more research active faculty, what really makes them elite is the quality of their students. It is not that elite colleges produce the best graduates but rather that the best students choose elite colleges. Now there is an over supply of gifted students. For every student that is admitted to a top ten school there are probably five or more others who would have done equally well. This is not entirely a negative thing. Having talent spread across more universities is a boon to students and society.
As seen with what happened in California and Michigan, eliminating race-conscious admission will likely decrease the number of under-represented minorities at elite schools. But this only matters if going to an elite school is the only way to access to the levers of power and have a productive life. We could make an elite education available to everyone. We could increase supply by increasing funding to state run universities and we could take away the public subsidy of elite private schools by taxing their land and endowments. The fact that affirmative action still matters over a half century later is an indication of failure. There is talent everywhere and that talent should be given a chance to flourish.
Chat GPT and the end of human culture
I had a personal situation this past year that kept me from posting much but today I decided to sit down and write something – all by myself without any help from anyone or anything. I could have enlisted the help of Chat GPT or some other large language model (LLM) but I didn’t. These posts generally start out with a foggy idea, which then take on a life of their own. Part of my enjoyment of writing these things is that I really don’t know what they will say until I’m finished. But sometime in the near future I’m pretty sure that WordPress will have a little window where you can type an idea and a LLM will just write the post for you. At first I will resist using it but one day I might not feel well and I’ll try it and like it and eventually all my posts will be created by a generative AI. Soon afterwards, the AI will learn what I like to blog about and how often I do so and it will just start posting on it’s own without my input. Maybe most or all content will be generated by an AI.
These LLMs are created by training a neural network to predict the next word of a sentence, given the previous words, sentences, paragraphs, and essentially everything that has ever been written. The machine is fed some text and produces what it thinks should come next. It then compares its prediction with the actual answer and updates its settings (connection weights) based on some score of how well it did. When fed the entire corpus of human knowledge (or at least what is online), we have all seen how well it can do. As I have speculated previously (see here), this isn’t all too surprising given that the written word is relatively new in our evolutionary history. Thus, humans aren’t really all that good at it and there isn’t all that much variety in what we write. Once an AI has the ability to predict the next word, it doesn’t take much more tinkering to make it generate an entire text. The specific technology that made this generative leap is called a diffusion model, which I may describe in more technical detail in the future. But in the simplest terms, the model finds successive small modifications to transform the initial text (or image or anything) into pure noise. The model can then be run backwards starting from random noise to create text.
When all content is generated by AI, the AI will no longer have any human data on which to further train. Human written culture will then be frozen. The written word will just consist of rehashing of previous thoughts along with random insertions generated by a machine. If the AI starts to train on AI generated text then it could leave human culture entirely. Generally, when these statistical learning machines train on their own generated data they can go unstable and become completely unpredictable. Will the AI be considered conscious by then?
New Paper
Distributing task-related neural activity across a cortical network through task-independent connections
Nature Communications volume 14, Article number: 2851 (2023) Cite this article
Abstract
Task-related neural activity is widespread across populations of neurons during goal-directed behaviors. However, little is known about the synaptic reorganization and circuit mechanisms that lead to broad activity changes. Here we trained a subset of neurons in a spiking network with strong synaptic interactions to reproduce the activity of neurons in the motor cortex during a decision-making task. Task-related activity, resembling the neural data, emerged across the network, even in the untrained neurons. Analysis of trained networks showed that strong untrained synapses, which were independent of the task and determined the dynamical state of the network, mediated the spread of task-related activity. Optogenetic perturbations suggest that the motor cortex is strongly-coupled, supporting the applicability of the mechanism to cortical networks. Our results reveal a cortical mechanism that facilitates distributed representations of task-variables by spreading the activity from a subset of plastic neurons to the entire network through task-independent strong synapses.
Milo Time
Milo Kessler died of osteosarcoma on March 11, 2022. He was just 18. He was a math major and loved tennis. I never met Milo but I think of him often. I got to know his father Daryl after Milo had passed. Daryl created this podcast about Milo. It’s very well done and gives me comfort.
Selection of the Day
How many different universes can there be?
If there are an infinite number of universes or even if a single universe is infinite in extent then each person (or thing) should have an infinite number of doppelgangers, each with a slight variation. The argument is that if the universe is infinite, and most importantly does not repeat itself, then all possible configurations of matter and energy (or bits of stuff) can and will occur. There should be an infinite number of other universe or other parts of our universe that contain another solar system, with a sun and an earth and a you except that maybe one molecule in one of your cells is in a different position or moving at a different velocity. A simple way to think about this is to imagine an infinite black and white TV screen where each pixel can be either black or white. If the screen is nonperiodic then any configuration of pixels can be found somewhere on the screen. This is kind of like how any sequence of numbers can be found in the digits of Pi or an infinite number of monkeys typing will eventually type out Hamlet. This generalizes to changing or time dependent universes where any sequence of flickering pixels will exist somewhere on the screen.
Not all universes are possible if you include any type of universal rule in your universe. Universes that violate the rule are excluded. If the pixels obeyed Newton’s law of motion then arbitrary sequences of pixels could no longer occur because the configuration of pixels in the next moment of time depends on the previous moment. However, we can have all possible worlds if we assume that rules are not universal and can change over different parts of the universe.
Some universes are also excluded if we introduce rational belief. For example, it is possible that there is another universe, like in almost every movie these days, that is like ours but slightly different. However, it is impossible for a purely rational person in a given universe to believe arbitrary things. Rational belief is as strong a constraint on the universe as any law of motion. One cannot believe in the conservation of energy and the Incredible Hulk (who can increase in mass by a factor of a thousand within seconds) at the same time. Energy is not universally conserved in the Marvel Cinematic Universe. (Why these supposedly super-smart scientists in those universes don’t invent a perpetual motion machine is a mystery.) Rationality does not even have to be universal. Just having a single rational person excludes certain universes. Science is impossible in a totally random universe in which nothing is predictable. However, if a person merely believed they were rational but were actually not then any possible universe is again possible.
Ultimately, this boils down to the question of what exactly exists? I for one believe that concepts such as rationality, beauty, and happiness exist as much as matter and energy exists. Thus for me, all possible universes cannot exist. There does not exist a universe where I am happy and there is so much suffering and pain in the world.
2023-12-28: Corrected a typo.
Falling through the earth part 2
In my previous post, I showed that an elevator falling from the surface through the center of the earth due to gravity alone would obey the dynamics of a simple harmonic oscillator. I did not know what would happen if the shaft went through some arbitrary chord through the earth. Rick Gerkin believed that it would take the same amount of time for all chords and it turns out that he is correct. The proof is very simple. Consider any chord (straight path) through the earth. Now take a plane and slice the earth through that chord and the center of the earth. This is always possible because it takes three points to specify a plane. Now looking perpendicular to the plane, you can always rotate the earth such that you see
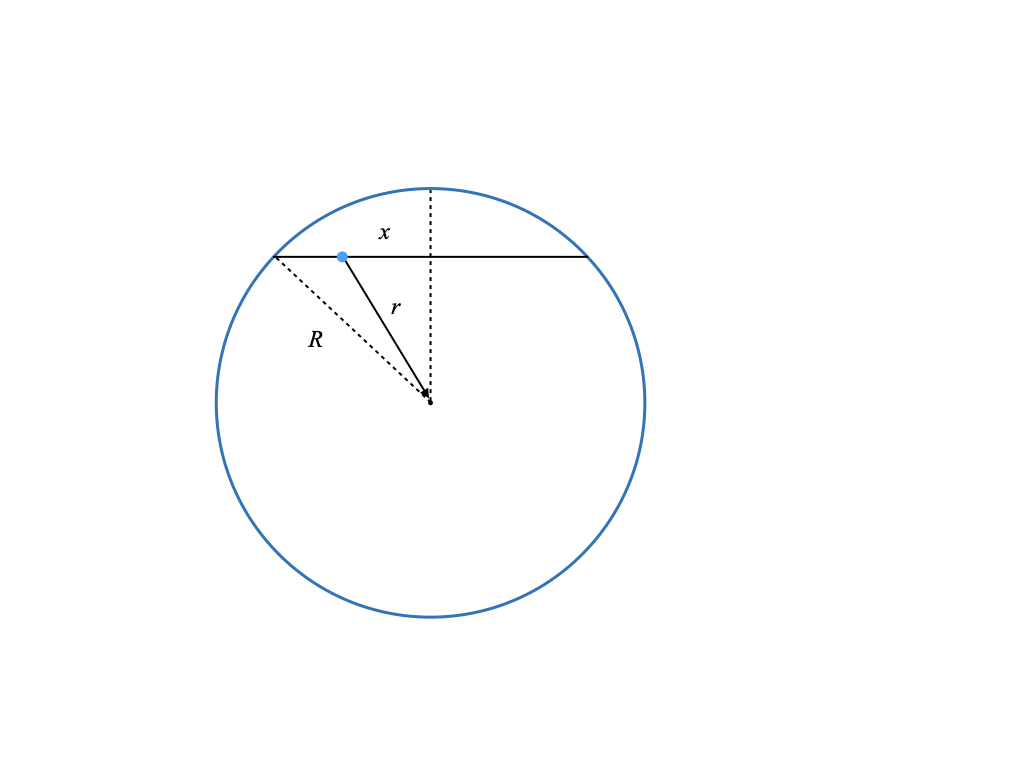
Let the blue dot represent the elevator on this chord. It will fall towards the midpoint. The total force on the elevator is towards the center of the earth along the vector . From the previous post, we know that the gravitational acceleration is
. The force driving the elevator is along the chord and will have a magnitude that is given by
times the cosine of the angle between
and
. But this has magnitude exactly equal to
! Thus, the acceleration of the elevator along the chord is
and thus the equation of motion for the elevator is
, which will be true for all chords and is the same as what we derived before. Hence, it will take the same amount of time to transit the earth. This is a perfect example of how most problems are solved by conceptualizing them in the right way.
Falling through the earth
The 2012 remake of the classic film Total Recall features a giant elevator that plunges through the earth from Australia to England. This trip is called the “fall”, which I presume to mean it is propelled by gravity alone in an evacuated tube. The film states that the trip takes 17 minutes (I don’t remember if this is to get to the center of the earth or the other side). It also made some goofy point that the seats flip around in the vehicle when you cross the center because gravity reverses. This makes no sense because when you fall you are weightless and if you are strapped in, what difference does it make what direction you are in. In any case, I was still curious to know if 17 minutes was remotely accurate and the privilege of a physics education is that one is given the tools to calculate the transit time through the earth due to gravity.
The first thing to do is to make an order of magnitude estimate to see if the time is even in the ballpark. For this you only need middle school physics. The gravitational acceleration for a mass at the surface of the earth is . The radius of the earth is 6.371 million metres. Using the formula that distance
(which you get by integrating twice over time), you get
. Plugging in the numbers gives 1140 seconds or 19 minutes. So it would take 19 minutes to get to the center of the earth if you constantly accelerated at
. It would take the same amount of time to get back to the surface. Given that the gravitational acceleration at the surface should be an upper bound, the real transit time should be slower. I don’t know who they consulted but 17 minutes is not too far off.
We can calculate a more accurate time by including the effect of the gravitational force changing as you transit through the earth but this will require calculus. It’s a beautiful calculation so I’ll show it here. Newton’s law for the gravitational force between a point mass m and a point mass M separated by a distance r is
where is the gravitational constant. If we assume that mass M (i.e. earth) is fixed then Newton’s 2nd law of motion for the mass m is given by
. The equivalence of inertial mass and gravitational mass means you can divide m from both sides. So, if a mass m were outside of the earth, then it would accelerate towards the earth as
and this number is g when r is the radius of the earth. This is the reason that all objects fall with the same acceleration, apocryphally validated by Galileo on the Tower of Pisa. (It is also the basis of the theory of general relativity).
However, the earth is not a point but an extended ball where each point of the ball exerts a gravitational force on any mass inside or outside of the ball. (Nothing can shield gravity). Thus to compute the force acting on a particle we need to integrate over the contributions of each point inside the earth. Assume that the density of the earth is constant so the mass
where
is the radius of the earth. The force between two point particles acts in a straight line between the two points. Thus for an extended object like the earth, each point in it will exert a force on a given particle in a different direction. So the calculation involves integrating over vectors. This is greatly simplified because a ball is highly symmetric. Consider the figure below, which is a cross section of the earth sliced down the middle.
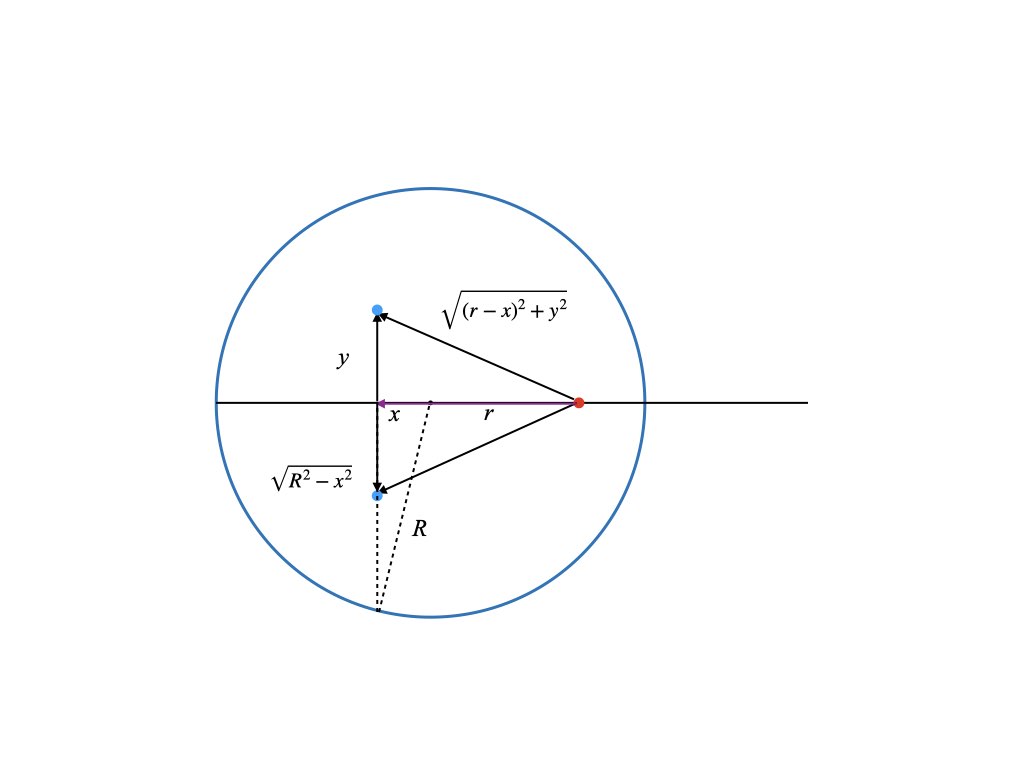
The particle/elevator is the red dot, which is located a distance r from the center. (It can be inside or outside of the earth). We will assume that it travels on an axis through the center of the earth. We want to compute the net gravitational force on it from each point in the earth along this central axis. All distances (positive and negative) are measured with respect to the center of the earth. The blue dot is a point inside the earth with coordinates (x,y). There is also the third coordinate coming out of the page but we will not need it. For each blue point on one side of the earth there is another point diametrically opposed to it. The forces exerted by the two blue points on the red point are symmetrical. Their contributions in the y direction are exactly opposite and cancel leaving the net force only along the x axis. In fact there is an entire circle of points with radius y (orthogonal to the page) around the central axis where each point on the circle combines with a partner point on the opposite side to yield a force only along the x axis. Thus to compute the net force on the elevator we just need to integrate the contribution from concentric rings over the volume earth. This reduces an integral over three dimensions to just two.
The magnitude of the force (density) between the blue and red dot is given by
To get the component of the force along the x direction we need to multiple by the cosine of the angle between the central axis and the blue dot, which is
(i.e. ratio of the adjacent to the hypotenuse of the relevant triangle). Now, to capture the contributions for all the pairs on the circle we multiple by the circumference which is . Putting this together gives
The y integral extends from zero to the edge of the earth, which is . (This is R at
(the center) and zero at
(the poles) as expected). The x integral extends from one pole to the other, hence -R to R. Completing the y integral gives
(*)
The second term comes from the 0 limit of the integral, which is . The square root of a number has positive and negative roots but the denominator here is a distance and thus is always a positive quantity and thus must include the absolute value. The first term of the above integral can be completed straightforwardly (I’ll leave it as an exercise) but the second term must be handled with care because r-x can change sign depending on whether r is greater or less than x. For a particle outside of the earth r-x is always positive and we get
Inside the earth, we must break the integral up into two parts
The first term of (*) integrates to
Using the fact that , we get
(We again need the absolute value sign). For , the particle is outside of the earth) and
. Putting everything together gives
Thus, we have explicitly shown that the gravitational force exerted by a uniform ball is equivalent to concentrating all the mass in the center. This formula is true for too.
For we have
Remarkably, the gravitational force on a particle inside the earth is just the force on the surface scaled by the ratio r/R. The equation of motion of the elevator is thus
with
(Recall that the gravitational acceleration at the surface is ). This is the classic equation for a harmonic oscillator with solutions of the form
. Thus, a period (i.e. round trip) is given by
. Plugging in the numbers gives 5062 seconds or 84 minutes. A transit through the earth once would be half that at 42 minutes and the time to fall to the center of the earth would be 21 minutes, which I find surprisingly close to the back of the envelope estimate.
Now Australia is not exactly antipodal to England so the tube in the movie did not go directly through the center, which would make the calculation much harder. This would be a shorter distance but the gravitational force would be at an angle to the tube so there would be less acceleration and something would need to keep the elevator from rubbing against the walls (wheels or magnetic levitation). I actually don’t know if it would take a shorter or longer time than going through the center. If you calculate it, please let me know.
The dynamics of inflation
Inflation, the steady increase of prices and wages, is a nice example of what is called a marginal mode, line attractor, or invariant manifold in dynamical systems. What this means is that the dynamical system governing wages and prices has an equilibrium that is not a single point but rather a line or curve in price and wage space. This is easy to see because if we suddenly one day decided that all prices and wages were to be denominated in some other currency, say Scooby Snacks, nothing should change in the economy. Instead of making 15 dollars an hour, you now make 100 Scooby Snacks an hour and a Starbucks Frappuccino will now cost 25 Scooby Snacks, etc. As long as wages and prices are in balance, it does not matter what they are denominated in. That is why the negative effects of inflation are more subtle than simply having everything cost more. In a true inflationary state your inputs should always balance your outputs but at an ever increasing price. Inflation is bad because it changes how you think about the future and that adjustments to the economy always take time and have costs.
This is why our current situation of price increases does not yet constitute inflation. We are currently experiencing a supply shock that has made goods scarce and thus prices have increased to compensate. Inflation will only take place when businesses start to increase prices and wages in anticipation of future increases. We can show this in a very simple mathematical model. Let P represent some average of all prices and W represent average wages (actually they will represent the logarithm of both quantities but that will not matter for the argument). So in equilibrium P = W. Now suppose there is some supply shock and prices now increase. In order to get back into equilibrium wages should increase so we can write this as
where the dot indicates the first derivative (i.e. rate of change of W is positive if P is greater than W). Similarly, if wages are higher than prices, prices should increase and we have
Now notice that the equilibrium (where there is no change in W or P) is given by W=P but given that there is only one equation and two unknowns, there is no unique solution. W and P can have any value as long as they are the same. W – P = 0 describes a line in W-P space and thus it is called a line attractor. (Mathematicians would call this an invariant manifold because a manifold is a smooth surface and the rate of change does not change (i.e. is invariant) on this surface. Physicists would call this a marginal mode because if you were to solve the eigenvalue equation governing this system, it would have a zero eigenvalue, which means that its eigenvector (called a mode) is on the margin between stable and unstable.) Now if you add the two equations together you get
which implies that the rate of change of the sum of P and W, which I call S, is zero. i.e. there is no inflation. Thus if prices and wages respond immediately to changes then there can be no inflation (in this simple model). Now suppose we have instead
The second derivative of W and P respond to differences. This is like having a delay or some momentum. Instead of the rate of S responding to price wage differences, the rate of the momentum of S reacts. Now when we add the two equations together we get
If we integrate this we now get
where C is some nonnegative constant. So in this situation, the rate of change of S is positive and thus S will just keep on increasing forever. Now what is C? Well it is the anticipatory increases in S. If you were lucky enough that C was zero (i.e. no anticipation) then there would be no inflation. Remember that W and P are logarithms so C is the rate of inflation. Interestingly, the way to combat inflation in this simple toy model is to add a first derivative term. This changes the equation to
which is analogous to adding friction to a mechanical system (used differently to what an economist would call friction). The first derivative counters the anticipatory effect of the second derivative. The solution to this equation will return to a state zero inflation (exercise to the reader).
Now of course this model is too simple to actually describe the real economy but I think it gives an intuition to what inflation is and is not.
2022-05-18: Typos corrected.
New Paper on Sars-CoV-2
Phase transitions may explain why SARS-CoV-2 spreads so fast and why new variants are spreading faster
J.C.Phillips, Marcelo A.Moret, Gilney F.Zebende, Carson C.Chow
Abstract
The novel coronavirus SARS CoV-2 responsible for the COVID-19 pandemic and SARS CoV-1 responsible for the SARS epidemic of 2002-2003 share an ancestor yet evolved to have much different transmissibility and global impact 1. A previously developed thermodynamic model of protein conformations hypothesized that SARS CoV-2 is very close to a new thermodynamic critical point, which makes it highly infectious but also easily displaced by a spike-based vaccine because there is a tradeoff between transmissibility and robustness 2. The model identified a small cluster of four key mutations of SARS CoV-2 that predicts much stronger viral attachment and viral spreading compared to SARS CoV-1. Here we apply the model to the SARS-CoV-2 variants Alpha (B.1.1.7), Beta (B.1.351), Gamma (P.1) and Delta (B.1.617.2)3 and predict, using no free parameters, how the new mutations will not diminish the effectiveness of current spike based vaccines and may even further enhance infectiousness by augmenting the binding ability of the virus.
https://www.sciencedirect.com/science/article/pii/S0378437122002576?dgcid=author
This paper is based on the ideas of physicist Jim Phillips, (formerly of Bell Labs, a National Academy member, and a developer of the theory behind Gorilla Glass used in iPhones). It was only due to Jim’s dogged persistence and zeal that I’m even on this paper although the persistence and zeal that ensnared me is the very thing that alienates most everyone else he tries to recruit to his cause.
Jim’s goal is to understand and characterize how a protein will fold and behave dynamically by utilizing an amino acid hydrophobicity (hydropathy) scale developed by Moret and Zebende. People have been developing hydropathy scores for many decades as a way to understand proteins with the idea that hydrophobic amino acids (residues) will tend to be on the inside of proteins while hydrophillic residues will be on the outside where the water is. There are several existing scores but Moret and Zebende, who are physicists and not chemists, took a different tack and found how the solvent-accessible surface area (ASA) scales with the size of a protein fragment with a specific residue in the center. The idea being that the smaller the ASA the more hydrophobic the residue. As protein fragments get larger they will tend to fold back on themselves and thus reduce the ASA. They looked at several thousand protein fragments and computed the average ASA with a given amino acid in the center. When they plotted the ASA vs length of fragment they found a power law and each amino acid had its own exponent. The more negative the exponent the smaller the ASA and thus the more hydrophobic the residue. The (negative) exponent could then be used as a hydropathy score. It differs from other scores in that it is not calculated in isolation based on chemical properties but accounts for the background of the amino acid.
M and Z’s score blew Jim’s mind because power laws are indicative of critical phenomena and phase transitions. Jim computed the coarse-grained hydropathy score (over a window of 35 residues) at each residue of a protein for a number of protein families. When COVID came along he naturally applied it to coronaviruses. He found that the coarse-grained hydropathy score profile of the spike protein of SARS-CoV-1 and SARS-CoV-2 had several deep hydrophobic wells. The well depths were nearly equal with SARS-CoV-2 being more equal than SARS-CoV-1. He then hypothesized that there was a selection advantage for well-depth symmetry and evolutionary pressure had pushed the SARS-CoV-2 spike to be near optimal. He argues that the symmetry allows the protein to coordinate activity better much like the way oscillators synchronize easier if their frequencies are more uniform. He predicted that given this optimality the spike was fragile and thus spike vaccines would be highly effective and that spike mutations could not change the spike much without diminishing function.
My contribution was to write some Julia code to automate this computation and apply it to some SARS-CoV-2 variants. I also scanned window sizes and found that the well depths are most equal close to Jim’s original value of 35. Below is Figure 3 from the paper.
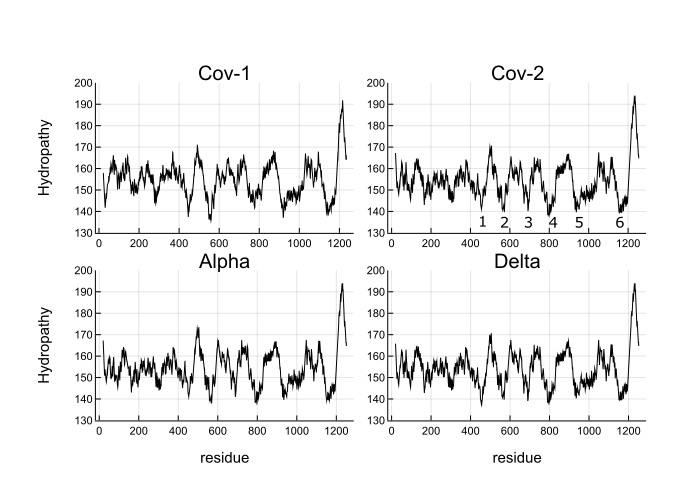
What you see is the coarse-grained hydropathy score of the spike protein which is a little under 1300 residues long. Between residue 400 and 1200 there are 6 hydropathic wells. The well depths are more similar for SARS-CoV-2 and variants than SARS-CoV-1. Omicron does not look much different from the wild type, which makes me think that Omicron’s increased infectiousness is probably due to mutations that affect viral growth and transmission rather than spike binding to ACE2 receptors.
Jim is encouraging (strong arming) me into pushing this further, which I probably will given that there are still so many unanswered questions as to how and why it works, if at all. If anyone is interested in this, please let me know.
Talk at Howard
Here are the slides for my talk at the “Howard University Math-Bio Virtual Workshop on Mitigation of Future Pandemics” last Saturday. One surprising thing (to me) the model predicted, shown on slide 40, is that the median fraction of those previously infected or vaccinated (or both) was 40% or higher during the omicron wave. I was pleased and relieved to then find that recent CDC serology results validate this prediction.
Reorganizing risk in the age of disaster
I’ve been thinking a lot about what we should do for the next (and current) disaster. The first thing to say is that I am absolutely positively sure that I could not have done any better than what had been done for Covid-19. I probably would have done things differently but I doubt it would have led to a better (and probably a worse) outcome. I still think in aggregate, we are doing about as well as we could have. The one thing I do think we need to do is to figure out a way to partition risk. The biggest problem of the current pandemic is that people do not realize or care that their own risky behavior puts other people at risk. I do not care if a person wants to jump off of a cliff in a bat suit because they are mostly taking the risk upon themselves (although they do take up a bed in an ER ward if they get injured). However, not wearing a mask or getting vaccinated puts other people, including strangers, at risk. If you knowingly attend a wedding with a respiratory illness then you have the potential to infect tens if not hundreds of people and killing a fraction of them.
I do think people should be allowed to take risks as long as there are limited consequences to others. Thus, in a pandemic I think we should figure out a way for people to not get vaccinated or wear masks without affecting others. Currently, the main bottleneck is the health care system. If we allow people to wantonly get infected then there is a risk that they overwhelm hospitals. This affects all people who may need healthcare. Now is not a good time to try to repair your roof because if you fall you may not be able to get a bed in an ER ward. Thus, we really do need to think about stratifying health care according to risk acceptance. People who choose to lead risky lives should get to the back of the line when it comes to treatment. These policies should be made clear. Those who refuse to be vaccinated should just sign a form that they could be delayed in receiving health care. If you want to attend a large gathering then you should sign the same waiver.
I think that people should be allowed to opt out of the Nanny State but they need to absorb the consequences. I personally like to live in a highly regulated state but I think people should have a choice to opt out. They can live in a flood zone if they wish but they should not be bailed out after the flood. If banks want to participate in risky activities then fine but we should not bail them out. We should have let every bank fail after the 2008 crisis. We could have just let them all go under and saved homeowners instead (who should have been made better aware of the risks they were taking). Bailing out banks was a choice not a necessity.
The dynamics of breakthrough infections
In light of the new omicron variant and breakthrough infections in people who have been vaccinated or previously infected, I was asked to discuss what a model would predict. The simplest model that includes reinfection is an SIRS model, where R, which stands for recovered, can become susceptible again. The equations have the form
I have ignored death due to infection for now. So like the standard SIR model, susceptible, S, have a chance of being infected, I, if they contact I. I then recovers to R but then has a chance to become S again. Starting from an initial condition of S = N and I very small, then S will decrease as I grows.
The first thing to note that the number of people N is conserved in this model (as it should be). You can see this by noting that the sum of the right hand sides of all the equations is zero. Thus and thus the integral is a constant and given that we started with N people then there will remain N people. This will change if we include births and deaths. Given this conservation law, then the dynamics have three possibilities. The first is that it goes to a fixed point meaning that in the long run the numbers of S, I and R will stabilize to some fixed number and remain there forever. The second is that it oscillates so S, I, and R will go up and down. The final one is that the orbit is chaotic meaning that S, I and R will change unpredictably. For these equations, the answer is the first option. Everything will settle to a fixed point.
To show this, you first must find an equilibrium or fixed point. You do this by setting all the derivatives to zero and solving the remaining equations. I have always found the fixed point to be the most miraculous state of any dynamical system. In a churning sea where variables move in all directions, there is one place that is perfectly still. The fixed point equations satisfy
There is a trivial fixed point given by S = N and I = R = 0. This is the case of no infection. However, if is large enough then this fixed point is unstable and any amount of I will grow. Assuming I is not zero, we can find another fixed point. Divide I out of the second equation and get
Solving the third equation gives us
which we can substitute into the first equation to get back the second equation. So to find I, we need to use the conservation condition S + I + R = N which after substituting for S and R gives
which we then back substitute to get
The fact that and
must be positive implies
is necessary.
The next question is whether this fixed point is stable. Just because a fixed point exists doesn’t mean it is stable. The classic example is a pencil balancing on its tip. Any small perturbation will knock it over. There are many mathematical definitions of stability but they essentially boil down to – does the system return to the equilibrium if you move away from it. The most straightforward way to assess stability is to linearize the system around the fixed point and then see if the linearized system grows or decays (or stays still). We linearize because linear systems are the only types of dynamical systems that can always be solved systematically. Generalizable methods to solve nonlinear systems do not exist. That is why people such as myself can devote a career to studying them. Each system is its own thing. There are standard methods you can try to use but there is no recipe that will always work.
To linearize around a fixed point we first transform to a coordinate system around that fixed point by defining ,
,
, to get
So now s = h = r = 0 is the fixed point. I used lower case h because lower case i is usually . The only nonlinear term is
, which we ignore when we linearize. Also by the definition of the fixed point
the system then simplifies to
which we can write as a matrix equation
, where
and
. The trace of the matrix is
so the sum of the eigenvalues is negative but the determinant is zero (since the rows sum to zero), and thus the product of the eigenvalues is zero. With a little calculation you can show that this system has two eigenvalues with negative real part and one zero eigenvalue. Thus, the fixed point is not linearly stable but could still be nonlinearly stable, which it probably is since the nonlinear terms are attracting.
That was a lot of tedious math to say that with reinfection, the simplest dynamics will lead to a stable equilibrium where a fixed fraction of the population is infected. The fraction increases with increasing or
and decreases with
. Thus, as long as the reinfection rate is much smaller than the initial infection rate (which it seems to be), we are headed for a situation where Covid-19 is endemic and will just keep circulating around forever. It may have a seasonal variation like the flu, which is still not well understood and is beyond the simple SIRS equation. If we include death in the equations then there is no longer a nonzero fixed point and the dynamics will just leak slowly towards everyone dying. However, if the death rate is slow enough this will be balanced by births and deaths due to other causes.
Autocracy and Star Trek
Like many youth of my generation, I watched the original Star Trek in reruns and Next Generation and Deep Space Nine in real time. I enjoyed the shows but can’t really claim to be a Trekkie. I was already in graduate school when Next Generation began so I could not help but to scrutinize the shows for scientific accuracy. I was impressed that the way they discovered life in a baby universe created in one episode was by detecting localized entropy reduction, which is quite sophisticated scientifically. I bristled each time the star ship was on the brink of total failure and about to explode but the artificial gravity system still didn’t fail. I celebrated the one episode that actually had an artificial gravity failure and people actually floated in space! I thought it was ridiculous that almost every single planet they visited was always at room temperature with a breathable atmosphere. That doesn’t even describe many parts of earth. I mostly let these inaccuracies slide in the interest of story but I could never let go of one thing that always left me feeling somewhat despondent about the human condition, which was that even in a supposed super advanced egalitarian democratic society where material shortages no longer existed, Star Fleet was still an absolute autocracy. Many of the episodes dealt with strictly obeying the chain of command and never disobeying direct orders. A world with a democratic federation of planets, transporters and faster than light travel still believed that autocracy was the most efficient way to run an organization.
For most people throughout history and including today, the difference between autocracy and democracy is mostly abstract. People go to jobs where a boss tells them what to do. Virtually no one questions that corporations should be run autocratically. Authoritarian CEO’s are celebrated. Religion is generally autocratic. It only makes sense that the military backs autocrats given that autocracy is already the governing principle of their enterprise. Julius Caesar crossed the Rubicon and became the Dictator of Rome (he was never actually made Emperor) because he had the biggest army and it was loyal to him, not the Roman Republic. The only real question is how democracies even persist. People may care about freedom but do they really care all that much about democracy?
My immune system
One outcome of the pandemic is that I have not had any illness (knock on wood), nary a cold nor sniffle, in a year and a half. On the other hand, my skin has fallen apart. I am constantly inflamed and itchy. I have no proof that the two are connected but my working hypothesis is that my immune system is hypersensitive right now because it has had little to do since the spring of 2020. It now overreacts to every mold spore, pollen grain, and speck of dust it runs into. The immune system is extremely complex, perhaps as complex as the brain. Its job is extremely difficult. It needs to recognize threats and eliminate them while not attacking itself. The brain and the immune system are intricately linked. How many people have gotten ill immediately after a final exam or deadline? The immune system was informed by the brain to delay action until the task was completed. The brain probably takes cues form the immune system too. One hypothesis for why asthma and allergies have been on the rise recently is that modern living has eliminated much contact with parasites and infectious agents, making the immune system hypersensitive. I for one, always welcome vaccinations because it gives my immune system something to do. In fact, I think it would be a good idea to get inoculations of all types regularly. I would take a vaccine for tape worm in a heartbeat. We are now slowly exiting from a global experiment in depriving the immune system of stimulation. We have no idea what the consequences will be. That is not to say that quarantine and isolation was not a good idea. Being itchy is clearly better than being infected by a novel virus (or being dead). There can be long term effects of infection too. Long covid is likely to be due to a miscalibrated immune system induced by the infection. Unfortunately, we shall likely never disentangle all the effects of COVID-19. We will not ever truly know what the long term consequences of infection, isolation, and vaccination will be. Most people will come out of this fine but a small fraction will not and we will not know why.
RNA
I read an article recently about an anti-vaccination advocate exclaiming at a press conference with the governor of Florida that vaccines against SARS-CoV-2 “change your RNA!” This made me think that most people probably do not know much about RNA and that a little knowledge is a dangerous thing. Now ironically, contrary to what the newspapers say, this statement is kind of true although in a trivial way. The Moderna and Pfizer vaccines insert a little piece of RNA into your cells (or rather cells ingest them) and that RNA gets translated into a SARS-CoV-2 spike protein that gets expressed on the surface of the cells and thereby presented to the immune system. So, yes these particular vaccines (although not all) have changed your RNA by adding new RNA to your cells. However, I don’t think this is what the alarmist was worried about. To claim that something that changes is a bad thing implies that the something is fixed and stable to start with, which is profoundly untrue about RNA.
The central dogma of molecular biology is that genetic information flows from DNA to RNA to proteins. All of your genetic material starts as DNA organized in 23 pairs of chromosomes. Your cells will under various conditions transcribe this DNA into RNA, which is then translated into proteins. The biological machinery that does all of this is extremely complex and not fully understood and part of my research is trying to understand this better. What we do know is that transcription is an extremely noisy and imprecise process at all levels. The molecular steps that transcribe DNA to RNA are stochastic. High resolution images of genes in the process of transcription show that transcription occurs in random bursts. RNA is very short-lived, lasting between minutes to at most a few days. There is machinery in the cell dedicated to degrading RNA. RNA is spliced; it is cut up into pieces and reassembled all the time and this splicing happens more or less randomly. Less than 2% of your DNA codes for proteins but virtually all of the DNA including noncoding parts are continuously being transcribed into small RNA fragments. Your cell is constantly littered with random stray pieces of RNA, and only a small fraction of it gets translated into proteins. Your RNA changes. All. The. Time.
Now, a more plausible alarmist statement (although still untrue) would be to say that vaccines change your DNA, which could be a bad thing. Cancer after all involves DNA mutations. There are viruses (retroviruses) that insert a copy of its RNA code into the host’s DNA. HIV does this for example. In fact, a substantial fraction of the human genome is comprised of viral genetic material. Changing proteins can also be very bad. Prion diseases are basically due to misfolded proteins. So DNA changing is not good, protein changing is not good, but RNA changing? Nothing to see here.
COVID, COVID, COVID
Even though Covid- is going to be with us forever, I actually think on the whole the pandemic turned out better than expected, and I mean that in the technical sense. If we were to rerun the pandemic over and over again, I think our universe will end up with fewer deaths than average. That is not to say we haven’t done anything wrong. We’ve botched up many things of course but given that the human default state is incompetence, we botched less than we could have.
The main mistake in my opinion was the rhetoric on masks in March of 2020. Most of the major Western health agencies recommended against wearing masks at that time because they 1) there was already a shortage of N95 masks for health care workers and 2) they thought that cloth and surgical masks were not effective in keeping one from being infected. Right there is a perfect example of Western solipsism; masks were only thought of as tools for self-protection, rather than as barriers for transmission. If only it was made clear early on that the reason we wear masks is not to protect me from you but to protect you from me. (Although there is evidence that masks do protect the wearer too, see here). This would have changed the rhetoric over masks we are having right now. The anti-maskers would be defending their right to harm others rather than the right to not protect themselves from harm.
The thing we got right was in producing effective vaccines. That was simply astonishing. There had never been a successful mRNA-based drug of any type until the BioNTech and Moderna vaccines. Many things had to go right for the vaccines to work. We needed a genetic sequence (Chinese scientists made it public in January), from that sequence we needed a target (the coronavirus spike protein), we needed to be able to stabilize the spike (research that came out of the NIH vaccine center), we needed to make mRNA less inflammatory (years of work especially at Penn), we needed a way to package that mRNA (work out of MIT), and we needed a sense of urgency to get it done (Western governments). Vaccines don’t always work but we managed to get one in less than a year. So many things had to go right for that to happen. The previous US administration should be taking a victory lap because it was developed under their watch, instead of bashing it.
As I’ve said before, I am skeptical we can predict what will happen next but I am going to predict now that there will not be a variant in the next year that will escape from our current vaccines. We may need booster shots and minor tweaks but the vaccines will continue to work. Part of my belief stems from the work of JC Phillips who argues that the SARS-CoV-2 spike protein is already highly optimized and thus there is not much room for it to change and to become infectious. The virus may mutate to replicate faster within the body but the spike will be relatively stable and thus remain a target for the vaccines. The delta variant wave we’re seeing now is a pandemic of the unvaccinated. I have no idea if those against vaccinations will have a change of heart but at some point everyone will be infected and have some immune protection. (I just hope they approve the vaccine for children before winter). SARS-CoV-2 will continue to circulate just like the way the flu strain from the 1918 pandemic still circulates but it won’t be the danger and menace it is now.