Month: November 2011

New paper on GPCRs

Carson Chow Bioinformatics, Evolution, Papers

New paper in PloS One:

Fatakia SN, Costanzi S, Chow CC (2011) Molecular Evolution of the Transmembrane Domains of G Protein-Coupled Receptors. PLoS ONE 6(11): e27813. doi:10.1371/journal.pone.0027813

Abstract

G protein-coupled receptors (GPCRs) are a superfamily of integral membrane proteins vital for signaling and are important targets for pharmaceutical intervention in humans. Previously, we identified a group of ten amino acid positions (called key positions), within the seven transmembrane domain (7TM) interhelical region, which had high mutual information with each other and many other positions in the 7TM. Here, we estimated the evolutionary selection pressure at those key positions. We found that the key positions of receptors for small molecule natural ligands were under strong negative selection. Receptors naturally activated by lipids had weaker negative selection in general when compared to small molecule-activated receptors. Selection pressure varied widely in peptide-activated receptors. We used this observation to predict that a subgroup of orphan GPCRs not under strong selection may not possess a natural small-molecule ligand. In the subgroup of MRGX1-type GPCRs, we identified a key position, along with two non-key positions, under statistically significant positive selection.

The pitfalls of obesity and cancer drugs

Carson Chow Medicine, Obesity, Opinion

The big medical news last week was that the US FDA revoked the use of the drug Avastin for the treatment of breast cancer.  The reason was that any potential efficacy did not outweigh the side effects.  Avastin is an anti-angiogenesis drug that blocks the formation of blood vessels by inhibiting the vascular endothelial growth factor VEGF-A.  This class of drugs is a big money-maker for the biotechnology firm Genentech and has been used in cancer treatments and for macular degeneration where it is called Lucentis.  Avastin will still be allowed for colorectal and lung cancer and physicians can still prescribe it off-label for breast cancer.  The strategy of targeting blood delivery as an anti-tumour strategy was pioneered by Judah Folkman.  He and collaborators also showed that adipose tissue mass (i.e. fat cells) can be regulated through controlling blood vessel growth (Rupnick et al., 2002) and this has been proposed as a potential therapy for obesity (e.g. Kolonin et al, 2004; barnhart et al. 2011).  However, the idea will probably not go very far because of potential severe side effects.

I think this episode illustrates a major problem in developing any type of drug for obesity and to some degree cancer.  I’ve posted  on the basic physiology and physics of weight change multiple times before (see here) so I won’t go into details here but suffice it to say that we get fat because we eat more than we burn.  Consider this silly analogy:  Suppose we have a car with an expandable gas tank and we seem to be overfilling it all the time so that it’s getting really big and heavy.  What should we do to lighten the car?  Well, there are three basic strategies: 1) We can put a hole in the gas tank so as we fill the tank gas just leaks out. 2) We can make the engine more inefficient so it burns gas faster or 3) We can put less gas in the car.  If you look at it this way, the first two strategies seem completely absurd but they are pursued all the time in obesity research.  The drug Orlistat blocks absorption of fat in the intestines, which basically tries to make the gas tank (and your bowels) leaky.  One of the most celebrated recent discoveries in obesity research was the discovery that human adults have brown fat.  This is a type of adipocyte that converts food energy directly into heat.  It is abundant in small mammals like rodents and babies (that’s why your  newborn is nice and warm) but was thought to disappear in adults. Now, various labs are trying to develop drugs that activate brown fat.  In essence they want to make us less efficient and turn us into heaters.   The third strategy of reducing input has also been tried and has failed various times.  Stimulants such as methampthetamines were found very early on to suppress appetite but turning people into speed addicts wasn’t a viable strategy.  A recent grand failure was the cannabinoid receptor CB-1 blocker Rimonabant.  It worked on the principle that since cannabis seems to enhance appetite, blocking it suppresses appetite. It does work but it also caused severe depression and suicidal thoughts.  Also, given that CB-1 is important in governing synaptic strengths, I’m sure there would have been bad long-term effects as well. I won’t bother telling the story of fen-phen.

It’s kind of easy to see why almost all obesity drug therapies will fail because they must target some important component of metabolism or neural function.  While we seem to have some unconscious controls of appetite and satiety, we can also easily override them (as I plan to do tomorrow for Thanksgiving).  Hence, any drug that targets some mechanism will likely either cause bad side effects or  be compensated by other mechanisms.  This also applies to some degree to cancer drugs, which must kill cancer cells while ignoring healthy cells.  This is why I tend not to get overly excited whenever another new discovery in obesity research is announced.

New paper

Carson Chow Computational neuroscience, Kinetic Theory, Papers, Physics

A new paper in Physical Review E is now available on line here.  In this paper Michael Buice and I show how you can derive an effective stochastic differential (Langevin) equation for a single element (e.g. neuron) embedded in a network by averaging over the unknown dynamics of the other elements. This then implies that given measurements from a single neuron, one might be able to infer properties of the network that it lives in.  We hope to show this in the future. In this paper, we perform the calculation explicitly for the Kuramoto model of coupled oscillators (e.g. see here) but it can be generalized to any network of coupled elements.  The calculation relies on the path or functional integral formalism Michael developed in his thesis and generalized at the NIH.  It is a nice application of what is called “effective field theory”, where new dynamics (i.e. action) are obtained by marginalizing or integrating out unwanted degrees of freedom.  The path integral formalism gives a nice platform to perform this averaging.  The resulting Langevin equation has a noise term that is nonwhite, non-Gaussian and multiplicative.  It is probably not something you would have guessed a priori.

 Michael A. Buice1,2 and Carson C. Chow11Laboratory of Biological Modeling, NIDDK, NIH, Bethesda, Maryland 20892, USA
2Center for Learning and Memory, University of  Texas at Austin, Austin, Texas, USA

Received 25 July 2011; revised 12 September 2011; published 17 November 2011

Complex systems are generally analytically intractable and difficult to simulate. We introduce a method for deriving an effective stochastic equation for a high-dimensional deterministic dynamical system for which some portion of the configuration is not precisely specified. We use a response function path integral to construct an equivalent distribution for the stochastic dynamics from the distribution of the incomplete information. We apply this method to the Kuramoto model of coupled oscillators to derive an effective stochastic equation for a single oscillator interacting with a bath of oscillators and also outline the procedure for other systems.

Published by the American Physical Society

URL: http://link.aps.org/doi/10.1103/PhysRevE.84.051120
DOI: 10.1103/PhysRevE.84.051120
PACS: 05.40.-a, 05.45.Xt, 05.20.Dd, 05.70.Ln

St. Petersburg Paradox

Carson Chow Economics, Mathematics, Probablity

The St. Petersburg Paradox is a problem in economics that was first proposed by Nicolas Bernoulli in 1713 in a letter.  It involves a lottery where you buy a ticket to play a game where a coin is flipped until heads comes up.  If heads comes up on the 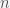nth toss you get 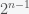2^{n-1} dollars.  So if heads comes up on the first toss you get one dollar and if it comes up on the fourth you would get 8 dollars.  The question is how much would you pay for a ticket to play this game.  In economics theory, the idea is that you would play if the expectation value of  the payout minus the ticket price is positive. The paradox for this game is that the expectation value of the payout is infinite but most people would pay no more than ten dollars.  The solution to the paradox  has been debated for the past three centuries.  Now, physicist Ole Peters argues that everyone before has missed a crucial  point and provides a new resolution to the paradox.  Peters also shows that a famous paper by Karl Menger in 1934 about this problem contains two critical errors that nullify Menger’s results.  I’ll give a summary of the mathematical analysis below, including my even simpler resolution.

The reason the expectation value of the payout is infinite is that the distribution is not normalizable. This can be seen easily because while the probability of getting 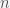n heads in a row decreases exponentially as p(n)=(1/2)^n, the payout increases exponentially as S(n)=2^{n-1}. The product is always 1/2 and never decays.  The expectation value is thus

E[S]=\sum_{n=1}^\infty p(n)S(n) = 1/2+1/2 + \cdots

and diverges.  The first proposed resolution of the paradox was by Daniel Bernoulli in a 1738  paper submitted to the Commentaries of the Imperial Academy of Science of St. Petersburg, from which the paradox received its name.  Bernoulli’s suggestion was that people don’t really value money linearly and proposed a utility function 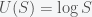U(S) = \log S, so the utility of money decreases with wealth. Given that this now grows sub-exponentially, the expectation value of U(S) is thus finite and resolves the paradox.  People have always puzzled over this solution because it seems ad hoc.  Why should my utility function be the same as someone else’s?  Menger suggested that he could always come up with an even faster growing payout function to make the expectation value still divergent and declared that all utility functions must be bounded.  According to Peters, this has affected the course of economics for the twentieth century and may have led to more risk taking than warranted mathematically.

Peter’s resolution is that the expectation value of the Bernoulli utility function is actually the time average of  the growth rate in wealth of a person that plays repeatedly.  Hence, if they pay more than a certain price they would certainly become bankrupt.  The proof is quite simple.  The factor by which a person’s wealth at round i changes is given by the expression

r_i = \frac{W_i-C+S_i}{W_i}

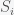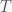where W_i is the wealth, C is the cost to play, and S_i is the payout at round i.  The total fractional change after T rounds is thus 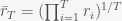\bar{r}_T=(\prod_{i=1}^T r_i)^{1/T}.  Now transform from rounds of the game played into 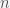n the number of tosses until the first heads.  This brings in the number of the occurrence of 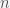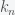n, k_n to yield

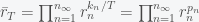\bar{r}_T= \prod_{n=1}^{n_{\infty}} r_n^{k_n/T}=\prod_{n=1}^{n_{\infty}} r_n^{p_n},

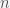where p_n is the probability for n tosses.  The average growth rate is given by taking the log, which gives the expression

\sum_{n=1}^\infty \left(\frac{1}{2}\right)^n (\ln(W-c+2^{n-1})-\ln W)

which is equivalent to the Bernoulli solution without the need for a utility function.

Now my solution, which has probably been proposed previously, is that we don’t really evaluate the expectation value of the payout but we take the payout of the expected number of tosses, which is a finite amount.  Thus we replace E(S(n)) with S(E(n)), where

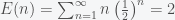E(n) =\sum_{n=1}^\infty n \left(\frac{1}{2}\right)^n=2,

which means we wouldn’t really want to play for more than 2 dollars. This might be a little conservative but it’s what I would do.

Another talk in Marseille

Carson Chow Computational neuroscience, Talks

I’m in beautiful Marseille again for a workshop on spike-timing dependent plasticity (STDP). My slides are here. The paper in which this talk is based can be obtained here. This paper greatly shaped how I think about neuroscience. I’ll give a summary of the paper and STDP for the uninitiated later.

Erratum: In my talk I said that I had reduced the models to disjunctive normal form. Actually, I had it backwards. I reduced it to conjunctive normal form. I’ll attribute this mixup to jet lag and lack of sleep.